Advertisements
Advertisements
प्रश्न
Derive an expression for drift velocity of free electrons.
Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm's law.
Advertisements
उत्तर
(i) Free electrons are in continuous random motion. They undergo change in direction at each collision and the thermal velocities are randomly distributed in all directions.
∴ Average thermal velocity,`u=(u_1+u_2+....+u_n)/n " is Zero".....(1)`
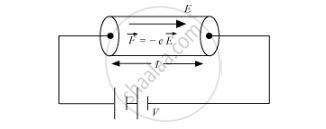
The electric field E exerts an electrostatic force ‘−Ee’.
Acceleration of each electron is,`veca=(-evecE)/m " ......(2)"`
Where,
m → Mass of an electron
e → Charge on an electron
Drift velocity,
`vec(v_d)=(vec(v_1)+vec(v_2)+....+vec(v_n))/n`
`vec(v_d)=((vec(u_1)+vecat_1)+(vec(u_2)+vecat_2)+....+(vec(u_n)+vecat_n))/n`
Where,
`vecu_1,vecu_2->` Thermal velocities of the electrons
`vecatau_1,vecatau_2->` Velocity acquired by electrons
τ1, τ2 → Time elapsed after the collision
`vec(v_d)=((vec(u_1)+vec(u_2)+...+vecu_n))/n+(veca(vec(t_1)+vec(t_2)+...vec(t_n)))/n`
Since `(vec(u_1)+vec(u_2)+....vec(u_n))/n=0`
∴ vd = a τ
Where,`t=(t_1+t_2+t_3....t_n)/n " is the average time elapsed"`
Substituting for a from equation (2),
`vec(v_d)=(-evecE)/mt " ...(4)"`
As, `E=V/l`
From (4) we can write
`v_d=(eV)/(ml)τ`
Also,
`I=An""ev_d`
Therefore,
`I=An""e((eV)/(ml)τ)=(An""e^2τ)/(ml) V`
`or V/I=(ml)/(An""e^2τ)=R` .... (5)
As we can see all the parameter on the R.H.S of the equation 5 are constant given temperature. And it is known as Resistance of the electric conductor.
APPEARS IN
संबंधित प्रश्न
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2·5 × 10−7 m2 carrying a current of 2·7 A. Assume the density of conduction electrons to be 9 × 1028 m−3
The number density of free electrons in a copper conductor is 8.5 × 1028 m−3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10−6 m2 and it is carrying a current of 3.0 A.
On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
Derive an expression for drift velocity of free electrons in a conductor in terms of relaxation time.
When a current is established in a wire, the free electrons drift in the direction opposite to the current. Does the number of free electrons in the wire continuously decrease?
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Peltier Effect is caused _______________ .
Metals are good conductor of heat than insulator because
Amount of charge in coulomb required to deposit one gram equivalent of substance by electrolysis is:-
Explain how free electrons in a metal at constant temperature attain an average velocity under the action of an electric field. Hence, obtain an expression for it.
A potential difference (V) is applied across a conductor of length 'L' and cross-sectional area 'A'.
How will the drift velocity of electrons and the current density be affected if another identical conductor of the same material were connected in series with the first conductor? Justify your answers.
