Advertisements
Advertisements
प्रश्न
(a) Write the basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus.
(b) In the reactions given below:
(i)`""_16^11C->_y^zB+x+v`
(ii)`""_6^12C+_6^12C->_a^20 Ne + _b^c He`
Find the values of x, y, and z and a, b and c.
उत्तर
(a)
The basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus
p →n + β++ v
For a beta-plus decay, a proton transforms into a neutron within the nucleus, according to the above reaction.
(b)
(i)
`""_6^11C->_y^zB+x+v`
`=>""_6^11C->_5^11B+_1^0beta+100`
The corresponding y and z are 5 and 11, respectively. The x is the positron
(ii)
`""_6^12C+_6^12C->_a^20 Ne +_b^c He`
⇒
`""_6^12C+_6^12C->_10^20Ne+_2^4He`
The corresponding values of a, b and c are 10, 2 and 4, respectively.
APPEARS IN
संबंधित प्रश्न
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
Define 'activity' of a radioactive substance ?
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
The radioactive isotope D decays according to the sequence
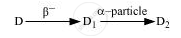
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of 14C averaged about 0.255 Bq per gram of carbon.
(a) What fraction of carbon atoms were 14C?
(b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? The half-life of 14C is 5730 years.
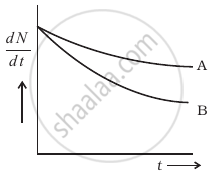
Which sample, A or B shown in figure has shorter mean-life?