Advertisements
Advertisements
प्रश्न
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
उत्तर
Given:
Half-life period of 40K, `T_"1/2"` = 1.30 × 109 years
Count given by 1 g of pure KCI, A = 160 counts/s
Disintegration constant, `lambda = 0.693/T_"1/2"`
Now, activity, A = λN
⇒ `160 = 0.693/t_"1/2" xx N`
⇒ `160 = (0.693/(1.30 xx 10^9 xx 365 xx 86400)) xx N`
⇒ `N = (160 xx 1.30 xx 365 xx 86400 xx 10^9)/0.693`
⇒ `N = 9.5 xx 10^18`
6.023 × 1023 atoms are present in 40 gm.
Thus , `9.5 xx 1018` atoms will be present in `(40 xx 9.5 xx 10^18)/(6.023 xx 10^23)` gm.
= `(4 xx 9.5 xx 10^-4)/6.023` gm
= `6.309 xx 10^-4`
= 0.00063 gm
Relative abundance of 40K in natural potassium = (2 × 0.00063 × 100)% = 0.12%
APPEARS IN
संबंधित प्रश्न
State the law of radioactive decay.
The Q value of a nuclear reaction A + b → C + d is defined by
Q = [mA+ mb − mC − md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^12_6C + ^12_6C ->^20_10Ne + ^4_2He}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12C)` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
Define 'activity' of a radioactive substance ?
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
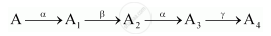
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
Lithium (Z = 3) has two stable isotopes 6Li and 7Li. When neutrons are bombarded on lithium sample, electrons and α-particles are ejected. Write down the nuclear process taking place.
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Define one Becquerel.
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
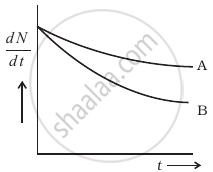
Which sample, A or B shown in figure has shorter mean-life?
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
The half-life of `""_82^210Pb` is 22.3 y. How long will it take for its activity 0 30% of the initial activity?
