Advertisements
Advertisements
प्रश्न
Which sample, A or B shown in figure has shorter mean-life?
Advertisements
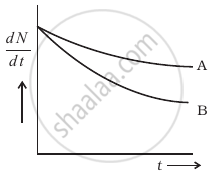
उत्तर
Mean (or average) life (ґ): The time for which a radioactive material remains active is defined as the mean (average) life of that material.
• It is defined as the sum of lives of all atoms divided by the total number of atoms.
i.e., `r = "Sum of the lives of all the atoms"/"Total number of atoms" = 1/λ`
• From `N = N_0e^(-λt)` ⇒ In `(N/N_0)/t = - λ`, the slope of the line shown in the graph, i.e., the magnitude of the inverse of slope of `N/N_0` vs t curve is known as mean life (τ).
• From `N = N_0e^(-λt)`, if `t = 1/λ = τ`
⇒ `N = N_0e^(-t) = N_0(1/e)` = 0.37 N0
= 37% of N0
i.e., mean life is the time interval in which the number of undecayed atoms (N) becomes `1/e` times or 0.37 times or 37% of the original number of atoms
• It is the time in which the number of decayed atoms (N0 – N) becomes `(1 - 1/e)` times or 0.63 times or 63% of the original number of atoms.
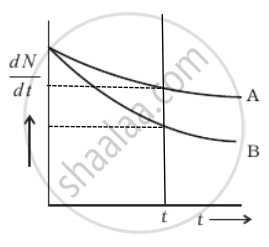
From the given figure, we can say that
At t = 0, `((dN)/(dt))_A = ((dN)/(dt))_B`
As `(dN)/(dt) = - λN`
⇒ (N0)A = (N0)B
Now considering any instant t by drawing a line perpendicular to the time axis, we find that `((dN)/(dt))_A > ((dN)/(dt))_B`
Hence, λANA = λBNB
∴ NA > NB ⇒ λB > λB ......[Rate of decay of B is slower]
But average life `τ = 1/λ` ⇒ τA > τB
APPEARS IN
संबंधित प्रश्न
State the law of radioactive decay.
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
A radioactive nucleus 'A' undergoes a series of decays as given below:
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
Why is it experimentally found difficult to detect neutrinos in this process ?
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
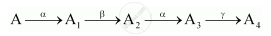
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
A radioactive isotope is being produced at a constant rate dN/dt = R in an experiment. The isotope has a half-life t1/2. Show that after a time t >> t1/2 the number of active nuclei will become constant. Find the value of this constant.
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of 14C averaged about 0.255 Bq per gram of carbon.
(a) What fraction of carbon atoms were 14C?
(b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? The half-life of 14C is 5730 years.
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
What percentage of radioactive substance is left after five half-lives?
Two electrons are ejected in opposite directions from radioactive atoms in a sample of radioactive material. Let c denote the speed of light. Each electron has a speed of 0.67 c as measured by an observer in the laboratory. Their relative velocity is given by ______.
The radioactivity of an old sample of whisky due to tritium (half-life 12.5 years) was found to be only about 4% of that measured in a recently purchased bottle marked 10 years old. The age of a sample is ______ years.
