Advertisements
Advertisements
प्रश्न
Which sample, A or B shown in figure has shorter mean-life?
Advertisements
उत्तर
Mean (or average) life (ґ): The time for which a radioactive material remains active is defined as the mean (average) life of that material.
• It is defined as the sum of lives of all atoms divided by the total number of atoms.
i.e., `r = "Sum of the lives of all the atoms"/"Total number of atoms" = 1/λ`
• From `N = N_0e^(-λt)` ⇒ In `(N/N_0)/t = - λ`, the slope of the line shown in the graph, i.e., the magnitude of the inverse of slope of `N/N_0` vs t curve is known as mean life (τ).
• From `N = N_0e^(-λt)`, if `t = 1/λ = τ`
⇒ `N = N_0e^(-t) = N_0(1/e)` = 0.37 N0
= 37% of N0
i.e., mean life is the time interval in which the number of undecayed atoms (N) becomes `1/e` times or 0.37 times or 37% of the original number of atoms
• It is the time in which the number of decayed atoms (N0 – N) becomes `(1 - 1/e)` times or 0.63 times or 63% of the original number of atoms.
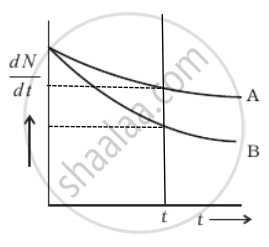
From the given figure, we can say that
At t = 0, `((dN)/(dt))_A = ((dN)/(dt))_B`
As `(dN)/(dt) = - λN`
⇒ (N0)A = (N0)B
Now considering any instant t by drawing a line perpendicular to the time axis, we find that `((dN)/(dt))_A > ((dN)/(dt))_B`
Hence, λANA = λBNB
∴ NA > NB ⇒ λB > λB ......[Rate of decay of B is slower]
But average life `τ = 1/λ` ⇒ τA > τB
APPEARS IN
संबंधित प्रश्न
Obtain the relation between the decay constant and half life of a radioactive sample.
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
The Q value of a nuclear reaction \[\ce{A + b → C + d}\] is defined by
Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12"C")` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
Lithium (Z = 3) has two stable isotopes 6Li and 7Li. When neutrons are bombarded on lithium sample, electrons and α-particles are ejected. Write down the nuclear process taking place.
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
Define the term 'decay constant' of a radioactive sample. The rate of disintegration of a given radioactive nucleus is 10000 disintegrations/s and 5,000 disintegrations/s after 20 hr. and 30 hr. respectively from start. Calculate the half-life and the initial number of nuclei at t= 0.
Define one Becquerel.
Disintegration rate of a sample is 1010 per hour at 20 hours from the start. It reduces to 6.3 x 109 per hour after 30 hours. Calculate its half-life and the initial number of radioactive atoms in the sample.
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
Draw a graph showing the variation of decay rate with number of active nuclei.
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
The radioactivity of an old sample of whisky due to tritium (half-life 12.5 years) was found to be only about 4% of that measured in a recently purchased bottle marked 10 years old. The age of a sample is ______ years.
