Advertisements
Advertisements
प्रश्न
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
विकल्प
all the containers will have 5000 atoms of the material.
all the containers will contain the same number of atoms of the material but that number will only be approximately 5000.
the containers will in general have different numbers of the atoms of the material but their average will be close to 5000.
none of the containers can have more than 5000 atoms.
उत्तर
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year the containers will in general have different numbers of the atoms of the material but their average will be close to 5000.
Explanation:
Half-life (T1/2): Radioactivity is a process due in which a radioactive material spontaneously decays. The time interval in which the mass of a radioactive substance or the number of its atom reduces to half of its initial value is called the half-life of the substance.
i.e., if `N = N_0/2`
Then t = T1/2
Hence from `N = N_0e^(-λt)`
`N_0/2 = N_0e^(-λ(T_(1/2))`
⇒ `T_(1/2) = (log_e 2)/λ = 0.693/λ`
In half-life (t = 1 yr) of the material on average half, the number of atoms will decay. Therefore, the containers will in general have different numbers of atoms of the material, but their average will be approx 5000.
APPEARS IN
संबंधित प्रश्न
Obtain the relation between the decay constant and half life of a radioactive sample.
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
A radioactive nucleus 'A' undergoes a series of decays as given below:
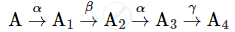
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
28Th emits an alpha particle to reduce to 224Ra. Calculate the kinetic energy of the alpha particle emitted in the following decay:
`""^228"Th" → ""^224"Ra"^(∗) + alpha`
`""^224"Ra"^(∗) → ""^224"Ra" + γ (217 "keV")`.
Atomic mass of 228Th is 228.028726 u, that of 224Ra is 224.020196 u and that of `""_2^4H` is 4.00260 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of `""_80^197`Hg (electron capture to `""_79^197`Au) is 1.8 × 10−4 S−1. (a) What is the half-life? (b) What is the average-life? (c) How much time will it take to convert 25% of this isotope of mercury into gold?
Define the term 'decay constant' of a radioactive sample. The rate of disintegration of a given radioactive nucleus is 10000 disintegrations/s and 5,000 disintegrations/s after 20 hr. and 30 hr. respectively from start. Calculate the half-life and the initial number of nuclei at t= 0.
A source contains two species of phosphorous nuclei, \[\ce{_15^32P}\] (T1/2 = 14.3 d) and \[\ce{_15^33P}\] (T1/2 = 25.3 d). At time t = 0, 90% of the decays are from \[\ce{_15^32P}\]. How much time has to elapse for only 15% of the decays to be from \[\ce{_15^32P}\]?
