Advertisements
Advertisements
प्रश्न
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
उत्तर
Half life of `""_15^32"P"`, T1/2 = 14.3 days
Half life of `""_15^33"P"`, T’1/2 = 25.3 days
`""_15^33"P"` nucleus decay is 10% of the total amount of decay.
The source has initially 10% of `""_15^33"P"` nucleus and 90% of `""_15^33"P"` nucleus.
Suppose after t days, the source has 10% of `""_15^32"P'` nucleus and 90% of `""_15^33"P"` nucleus.
Initially:
Number of `""_15^33"P"` nucleus = N
Number of `""_15^32"P"` nucleus = 9 N
Finally:
Number of `""_15^33"P"` nucleus = 9N
Number of `""_15^32"P"` nucleus = N
For `""_15^32"P"` nucleus, we can write the number ratio as:
`"N'"/(9"N'") = (1/2)^("t"/"T"_(1//2))`
`"N'" = 9"N" (2)^(-1/14.3)` ....(1)
For `""_15^33"P"` we can write the number ratio as:
`9"N'" = "N"(2)^(-1/(25.3))` ...(2)
On dividing equation (1) by equation (2), we get:
`1/9 = 9 xx 2^(("t"/25.3 - "t"/14.3))`
`1/18 = 2^(-((11"t")/(25.3 xx 14.3)))`
log 1 - log 81 = `(-11"t")/(25.3 xx 14.3)` log 2
`(-11"t")/(25.3 xx 14.3) = (0 - 1.908)/(0.301)`
t = `(25.3 xx 14.3 xx 1.908)/11 xx 0.301 ~~ 208.5` day
Hence, it will take about 208.5 days for 90% decay of `""_15"P"^33`.
APPEARS IN
संबंधित प्रश्न
The decay constant of radioactive substance is 4.33 x 10-4 per year. Calculate its half life period.
State the law of radioactive decay.
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
Obtain the relation between the decay constant and half life of a radioactive sample.
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
A radioactive nucleus 'A' undergoes a series of decays as given below:
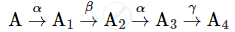
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
Lithium (Z = 3) has two stable isotopes 6Li and 7Li. When neutrons are bombarded on lithium sample, electrons and α-particles are ejected. Write down the nuclear process taking place.
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
A radioactive element disintegrates for an interval of time equal to its mean lifetime. The fraction that has disintegrated is ______
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
