Advertisements
Advertisements
Question
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
Solution
Half life of `""_15^32"P"`, T1/2 = 14.3 days
Half life of `""_15^33"P"`, T’1/2 = 25.3 days
`""_15^33"P"` nucleus decay is 10% of the total amount of decay.
The source has initially 10% of `""_15^33"P"` nucleus and 90% of `""_15^33"P"` nucleus.
Suppose after t days, the source has 10% of `""_15^32"P'` nucleus and 90% of `""_15^33"P"` nucleus.
Initially:
Number of `""_15^33"P"` nucleus = N
Number of `""_15^32"P"` nucleus = 9 N
Finally:
Number of `""_15^33"P"` nucleus = 9N
Number of `""_15^32"P"` nucleus = N
For `""_15^32"P"` nucleus, we can write the number ratio as:
`"N'"/(9"N'") = (1/2)^("t"/"T"_(1//2))`
`"N'" = 9"N" (2)^(-1/14.3)` ....(1)
For `""_15^33"P"` we can write the number ratio as:
`9"N'" = "N"(2)^(-1/(25.3))` ...(2)
On dividing equation (1) by equation (2), we get:
`1/9 = 9 xx 2^(("t"/25.3 - "t"/14.3))`
`1/18 = 2^(-((11"t")/(25.3 xx 14.3)))`
log 1 - log 81 = `(-11"t")/(25.3 xx 14.3)` log 2
`(-11"t")/(25.3 xx 14.3) = (0 - 1.908)/(0.301)`
t = `(25.3 xx 14.3 xx 1.908)/11 xx 0.301 ~~ 208.5` day
Hence, it will take about 208.5 days for 90% decay of `""_15"P"^33`.
APPEARS IN
RELATED QUESTIONS
How is the mean life of a given radioactive nucleus related to the decay constant?
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
A radioactive nucleus 'A' undergoes a series of decays as given below:
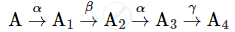
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
Why is it experimentally found difficult to detect neutrinos in this process ?
Define the activity of a given radioactive substance. Write its S.I. unit.
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
The half-life of the radioactive substance is 40 days. The substance will disintegrate completely in
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
Draw a graph showing the variation of decay rate with number of active nuclei.
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
