Advertisements
Advertisements
Question
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
Solution
The given nuclear reaction is:
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\]
Half life of `""_6^11C` nuclei `"T"_(1/2)` = 20.3 min
Atomic mass of `"m"(""_6^11"C")`= 11.011434 u
Atomic mass of `"m"(""_6^11"B") = 11.009305 "u"`
Maximum energy possessed by the emitted positron = 0.960 MeV
The change in the Q-value (ΔQ) of the nuclear masses of the `""_6^11"C"` nucleus is given as:
`triangle "Q" = ["m'"(""_6"C"^11) - ["m'"(""_5^11"B") + "m"_"e"]]"c"^2` ...(1)
Where,
me = Mass of an electron or positron = 0.000548 u
c = Speed of light
m’ = Respective nuclear masses
If atomic masses are used instead of nuclear masses, then we have to add 6 me in the case of `""^11"C"` and 5 me in the case of `""^11"B"`.
Hence, equation (1) reduces to:
`triangle"Q" = ["m"(""_6"C"^11) - "m"(""_5^11"B") - 2"m"]"c"^2` are the atomic masses
Here `"m"(""_6"C"^11) and "m'(""_5^11"B")` are the atomic masses
∴ Δ Q = [11.011434 − 11.009305 − 2 × 0.000548] c2
= (0.001033 c2) u
But 1 u = 931.5 Mev/c2
∴ Δ Q = 0.001033 × 931.5 ≈ 0.962 MeV
The value of Q is almost comparable to the maximum energy of the emitted positron.
APPEARS IN
RELATED QUESTIONS
(a) Write the basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus.
(b) In the reactions given below:
(i)`""_16^11C->_y^zB+x+v`
(ii)`""_6^12C+_6^12C->_a^20 Ne + _b^c He`
Find the values of x, y, and z and a, b and c.
Why is it found experimentally difficult to detect neutrinos in nuclear β-decay?
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
Identify the nature of the radioactive radiations emitted in each step of the decay process given below.
`""_Z^A X -> _Z^A _-1^-4 Y ->_Z^A _-1^-4 W`
Define one Becquerel.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
A source contains two species of phosphorous nuclei, \[\ce{_15^32P}\] (T1/2 = 14.3 d) and \[\ce{_15^33P}\] (T1/2 = 25.3 d). At time t = 0, 90% of the decays are from \[\ce{_15^32P}\]. How much time has to elapse for only 15% of the decays to be from \[\ce{_15^32P}\]?
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
A radioactive element disintegrates for an interval of time equal to its mean lifetime. The fraction that has disintegrated is ______
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
What percentage of radioactive substance is left after five half-lives?
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom ______.
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
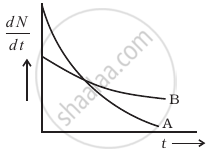
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
The half-life of `""_82^210Pb` is 22.3 y. How long will it take for its activity 0 30% of the initial activity?
