Advertisements
Advertisements
Question
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
Solution
Given:
Initial activity of charcoal, A0 = 15.3 disintegrations per gram per minute
Half-life of charcoal, `T_"1/2"` = 5730 years
Final activity of charcoal after a few years, A = 12.3 disintegrations per gram per minute
Disintegration constant, `lambda = 0.693/T_"1/2" = 0.693/5370 "y"^-1`
Let the sample take a time of t years for the activity to reach 12.3 disintegrations per gram per minute.
Activity of the sample, `A = A_0e^(-lambdat)`
`A = A_0e^(-0.693/5730 xx t)`
⇒`"In" 12.3/15.3 = (-0.693)/5730 t`
⇒ `0.218253 = 0.693/5730 t`
⇒ t = 1804.3 years
APPEARS IN
RELATED QUESTIONS
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
How is the mean life of a given radioactive nucleus related to the decay constant?
Why is it found experimentally difficult to detect neutrinos in nuclear β-decay?
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
The Q value of a nuclear reaction \[\ce{A + b → C + d}\] is defined by
Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12"C")` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
A radioactive nucleus 'A' undergoes a series of decays as given below:
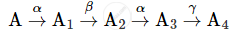
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
Why is it experimentally found difficult to detect neutrinos in this process ?
Define the activity of a given radioactive substance. Write its S.I. unit.
The radioactive isotope D decays according to the sequence
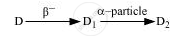
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
Lithium (Z = 3) has two stable isotopes 6Li and 7Li. When neutrons are bombarded on lithium sample, electrons and α-particles are ejected. Write down the nuclear process taking place.
Calculate the maximum kinetic energy of the beta particle emitted in the following decay scheme:
12N → 12C* + e+ + v
12C* → 12C + γ (4.43MeV).
The atomic mass of 12N is 12.018613 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of `""_80^197`Hg (electron capture to `""_79^197`Au) is 1.8 × 10−4 S−1. (a) What is the half-life? (b) What is the average-life? (c) How much time will it take to convert 25% of this isotope of mercury into gold?
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
Identify the nature of the radioactive radiations emitted in each step of the decay process given below.
`""_Z^A X -> _Z^A _-1^-4 Y ->_Z^A _-1^-4 W`
Define one Becquerel.
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
