Advertisements
Advertisements
Question
Calculate the maximum kinetic energy of the beta particle emitted in the following decay scheme:
12N → 12C* + e+ + v
12C* → 12C + γ (4.43MeV).
The atomic mass of 12N is 12.018613 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Solution
Given:-
Atomic mass of 12N, m(12N) = 12.018613 u
12N → 12C* + e+ + v
12C* → 12C + γ (4.43 MeV)
Net reaction is given by
12N → 12C + e+ + v + γ (4.43 MeV)
Qvalue of the `β^+` decay will be
Qvalue = [m(`""^12N`) - (m(12C*) + 2me)]c2
`= [12.018613 xx 931 "MeV" - (12 xx 931 + 4.43) "MeV" - (2 xx 511) "keV"]`
= [11189.3287 - 11176.43 - 1.022] MeV
`= 11.8767 "MeV" = 11.88 "MeV"`
The maximum kinetic energy of beta particle will be 11.88 MeV, assuming that neutrinos have zero energy.
APPEARS IN
RELATED QUESTIONS
The decay constant of radioactive substance is 4.33 x 10-4 per year. Calculate its half life period.
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
How is the mean life of a given radioactive nucleus related to the decay constant?
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
The Q value of a nuclear reaction \[\ce{A + b → C + d}\] is defined by
Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12"C")` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
A radioactive nucleus 'A' undergoes a series of decays as given below:
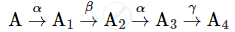
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
Define 'activity' of a radioactive substance ?
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
Lithium (Z = 3) has two stable isotopes 6Li and 7Li. When neutrons are bombarded on lithium sample, electrons and α-particles are ejected. Write down the nuclear process taking place.
A radioactive isotope is being produced at a constant rate dN/dt = R in an experiment. The isotope has a half-life t1/2. Show that after a time t >> t1/2 the number of active nuclei will become constant. Find the value of this constant.
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
Identify the nature of the radioactive radiations emitted in each step of the decay process given below.
`""_Z^A X -> _Z^A _-1^-4 Y ->_Z^A _-1^-4 W`
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
Disintegration rate of a sample is 1010 per hour at 20 hours from the start. It reduces to 6.3 x 109 per hour after 30 hours. Calculate its half-life and the initial number of radioactive atoms in the sample.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
