Advertisements
Advertisements
Question
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
Solution
Take a `""_6^14"C"` emission nuclear reaction:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
We know that:
Mass of `""_88^223"Ra"` m1 = 223.01850 u
Mass of `""_82^209"Pb"` m2 = 208.98107 u
Mass of `""_6^14"C"`, m3 = 14.00324 u
Hence, the Q-value of the reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 208.98107 − 14.00324) c2
= (0.03419 c2) u
But 1 u = 931.5 MeV/c2
∴ Q = 0.03419 × 931.5
= 31.848 MeV
Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed.
Now take a `""_2^4"He"` emission nuclear reaction:
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
We know that:
Mass of `""_88^223"Ra"`, m1 = 223.01850
Mass of `""_82^219"Rn"` m2 = 219.00948
Mass of `""_2^4"He"`, m3 = 4.00260
Q-value of this nuclear reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 219.00948 − 4.00260) C2
= (0.00642 c2) u
= 0.00642 × 931.5 = 5.98 MeV
Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed.
APPEARS IN
RELATED QUESTIONS
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
A radioactive nucleus 'A' undergoes a series of decays as given below:
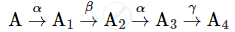
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
Define 'activity' of a radioactive substance ?
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
'Half-life' of a radioactive substance accounts for ______.
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
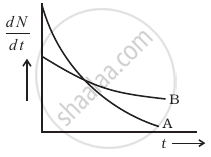
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
