Advertisements
Advertisements
प्रश्न
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
उत्तर
Take a `""_6^14"C"` emission nuclear reaction:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
We know that:
Mass of `""_88^223"Ra"` m1 = 223.01850 u
Mass of `""_82^209"Pb"` m2 = 208.98107 u
Mass of `""_6^14"C"`, m3 = 14.00324 u
Hence, the Q-value of the reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 208.98107 − 14.00324) c2
= (0.03419 c2) u
But 1 u = 931.5 MeV/c2
∴ Q = 0.03419 × 931.5
= 31.848 MeV
Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed.
Now take a `""_2^4"He"` emission nuclear reaction:
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
We know that:
Mass of `""_88^223"Ra"`, m1 = 223.01850
Mass of `""_82^219"Rn"` m2 = 219.00948
Mass of `""_2^4"He"`, m3 = 4.00260
Q-value of this nuclear reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 219.00948 − 4.00260) C2
= (0.00642 c2) u
= 0.00642 × 931.5 = 5.98 MeV
Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed.
APPEARS IN
संबंधित प्रश्न
The decay constant of radioactive substance is 4.33 x 10-4 per year. Calculate its half life period.
State the law of radioactive decay.
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
A radioactive nucleus 'A' undergoes a series of decays as given below:
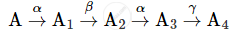
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of 14C averaged about 0.255 Bq per gram of carbon.
(a) What fraction of carbon atoms were 14C?
(b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? The half-life of 14C is 5730 years.
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
Which one of the following nuclei has shorter meant life?
'Half-life' of a radioactive substance accounts for ______.
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
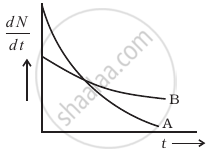
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
Draw a graph showing the variation of decay rate with number of active nuclei.
