Advertisements
Advertisements
प्रश्न
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
उत्तर
Given:-
Mass of 11C, m(11C) = 11.0114 u
Mass of 11B, m(11B) = 11.0093 u
Energy liberated in the β+ decay (Q) is given by
`Q = [m(""^11C) - m(""^11B) - 2m_e]c^2`
= (11.0114 u − 11.0093 u - 2 × 0.0005486 u)c2
= 0.0010028 × 931 MeV
= 0.9336 MeV = 933.6 keV
For maximum KE of the positron, energy of neutrino can be taken as zero.
∴ Maximum KE of the positron = 933.6 keV
APPEARS IN
संबंधित प्रश्न
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
The decay constant of `""_80^197`Hg (electron capture to `""_79^197`Au) is 1.8 × 10−4 S−1. (a) What is the half-life? (b) What is the average-life? (c) How much time will it take to convert 25% of this isotope of mercury into gold?
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
Disintegration rate of a sample is 1010 per hour at 20 hours from the start. It reduces to 6.3 x 109 per hour after 30 hours. Calculate its half-life and the initial number of radioactive atoms in the sample.
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
'Half-life' of a radioactive substance accounts for ______.
Two electrons are ejected in opposite directions from radioactive atoms in a sample of radioactive material. Let c denote the speed of light. Each electron has a speed of 0.67 c as measured by an observer in the laboratory. Their relative velocity is given by ______.
The half-life of the radioactive substance is 40 days. The substance will disintegrate completely in
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
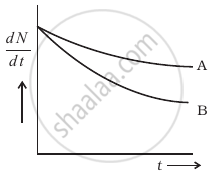
Which sample, A or B shown in figure has shorter mean-life?
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
The half-life of `""_82^210Pb` is 22.3 y. How long will it take for its activity 0 30% of the initial activity?
