Advertisements
Advertisements
प्रश्न
Disintegration rate of a sample is 1010 per hour at 20 hours from the start. It reduces to 6.3 x 109 per hour after 30 hours. Calculate its half-life and the initial number of radioactive atoms in the sample.
उत्तर
Data: A(t1) = 1010 per hour, where t1 = 20 h,
A(t1) = 6.3 × 1010 per hour, where t2 = 30 h
A(t) = A0e-λt ∴ A(t1) = `"A"_0"e"^(-λ"t"_1)` and
A(t2) = `"A"_0"e"^(-λ"t"_2)`
∴ `("A"("t"_1))/("A"("t"_2)) = ("e"^(-lambda"t"_1)/"e"^(-lambda"t"_2)) = "e"^(lambda("t"_2 - "t"_1))`
∴ `10^10/(6.3 xx 10^9) = "e"^(lambda(30 - 20)) = "e"^(10lambda)`
∴ 1.587 = e10λ
∴ 10λ = 2.303 log10(1.587)
∴ λ = (0.2303)(0.2007) = 0.04622 per hour
The half life of the material, T1/2 = `0.693/lambda = 0.693/0.04622`
= 14.99 hours
Now, `"A"_0 = "A"("t"_1)"e"^(lambda"t"_1) = 10^10"e"^((0.04622)(20))`
= `10^10 "e"^0.9244`
Let x = `"e"^0.9244`
∴ 2.303 log10x = 0.9244
∴ log10x = `0.9244/2.303 = 0.4014`
∴ x = antilog 0.4014 = 2.52
∴ A0 = 2.52 x 1010 per hour
Now A0 = N0λ
∴ `"N"_0 = "A"_0/lambda = (2.52 xx 10^10)/0.04622`
= 5.452 × 1011
APPEARS IN
संबंधित प्रश्न
(a) Write the basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus.
(b) In the reactions given below:
(i)`""_16^11C->_y^zB+x+v`
(ii)`""_6^12C+_6^12C->_a^20 Ne + _b^c He`
Find the values of x, y, and z and a, b and c.
State the law of radioactive decay.
How is the mean life of a given radioactive nucleus related to the decay constant?
Obtain the relation between the decay constant and half life of a radioactive sample.
Why is it found experimentally difficult to detect neutrinos in nuclear β-decay?
A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value?
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive `""_6^14"C"` present with the stable carbon isotope `""_6^12"C"`. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of `""_6^14"C"` and the measured activity, the age of the specimen can be approximately estimated. This is the principle of `""_6^14"C"` dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
The Q value of a nuclear reaction A + b → C + d is defined by
Q = [mA+ mb − mC − md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^12_6C + ^12_6C ->^20_10Ne + ^4_2He}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12C)` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
A radioactive nucleus 'A' undergoes a series of decays as given below:
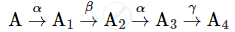
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
Define 'activity' of a radioactive substance ?
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
Why is it experimentally found difficult to detect neutrinos in this process ?
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
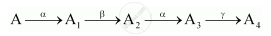
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
The radioactive isotope D decays according to the sequence
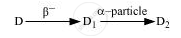
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
28Th emits an alpha particle to reduce to 224Ra. Calculate the kinetic energy of the alpha particle emitted in the following decay:
`""^228"Th" → ""^224"Ra"^(∗) + alpha`
`""^224"Ra"^(∗) → ""^224"Ra" + γ (217 "keV")`.
Atomic mass of 228Th is 228.028726 u, that of 224Ra is 224.020196 u and that of `""_2^4H` is 4.00260 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of `""_80^197`Hg (electron capture to `""_79^197`Au) is 1.8 × 10−4 S−1. (a) What is the half-life? (b) What is the average-life? (c) How much time will it take to convert 25% of this isotope of mercury into gold?
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
'Half-life' of a radioactive substance accounts for ______.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
What percentage of radioactive substance is left after five half-lives?
Two electrons are ejected in opposite directions from radioactive atoms in a sample of radioactive material. Let c denote the speed of light. Each electron has a speed of 0.67 c as measured by an observer in the laboratory. Their relative velocity is given by ______.
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom ______.
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
The radioactivity of an old sample of whisky due to tritium (half-life 12.5 years) was found to be only about 4% of that measured in a recently purchased bottle marked 10 years old. The age of a sample is ______ years.
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
