Advertisements
Advertisements
प्रश्न
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
पर्याय
1/λ and (In 2/λ)
(In 2/λ) and 1/λ
λ(In 2) and 1/λ
λ/(In 2) and 1/λ.
उत्तर
(ln 2/λ) and 1/λ
The half-life of a radioactive sample `(t_(1"/"2))` is defined as the time elapsed before half the active nuclei decays.
Let the initial number of the active nuclei present in the sample be `N_0` .
`N_0/2 = N_0e^(-lambdat_"1/2")`
⇒ `t_"1/2" = ("In 2")/lambda`
Average life of the nuclei, `t_(av) = S/N_0 = 1/lambda`
Here, S is the sum of all the lives of all the N nuclei that were active at t = 0 and `lambda` is the decay constant of the sample.
APPEARS IN
संबंधित प्रश्न
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
The Q value of a nuclear reaction A + b → C + d is defined by
Q = [mA+ mb − mC − md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^12_6C + ^12_6C ->^20_10Ne + ^4_2He}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12C)` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
A radioactive nucleus 'A' undergoes a series of decays as given below:
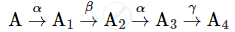
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
Why is it experimentally found difficult to detect neutrinos in this process ?
Define the activity of a given radioactive substance. Write its S.I. unit.
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
Lithium (Z = 3) has two stable isotopes 6Li and 7Li. When neutrons are bombarded on lithium sample, electrons and α-particles are ejected. Write down the nuclear process taking place.
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Calculate the maximum kinetic energy of the beta particle emitted in the following decay scheme:
12N → 12C* + e+ + v
12C* → 12C + γ (4.43MeV).
The atomic mass of 12N is 12.018613 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
The half-life of the radioactive substance is 40 days. The substance will disintegrate completely in
When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom ______.
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
The radioactivity of an old sample of whisky due to tritium (half-life 12.5 years) was found to be only about 4% of that measured in a recently purchased bottle marked 10 years old. The age of a sample is ______ years.
