Advertisements
Advertisements
प्रश्न
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
पर्याय
6 h
12 h
24 h
128 h.
उत्तर
12 h
A freshly prepared radioactive source emits radiation of intensity that is 64 times the permissible level. This means that it is possible to work safely till 6 half-lives (as 26 = 64) of the radioactive source. Since the half-life of the source is 2h, the minimum time after which it would be possible to work safely with this source is 12 h.
APPEARS IN
संबंधित प्रश्न
How is the mean life of a given radioactive nucleus related to the decay constant?
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
Calculate the maximum kinetic energy of the beta particle emitted in the following decay scheme:
12N → 12C* + e+ + v
12C* → 12C + γ (4.43MeV).
The atomic mass of 12N is 12.018613 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Define one Becquerel.
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
The isotope \[\ce{^57Co}\] decays by electron capture to \[\ce{^57Fe}\] with a half-life of 272 d. The \[\ce{^57Fe}\] nucleus is produced in an excited state, and it almost instantaneously emits gamma rays.
(a) Find the mean lifetime and decay constant for 57Co.
(b) If the activity of a radiation source 57Co is 2.0 µCi now, how many 57Co nuclei does the source contain?
c) What will be the activity after one year?
A radioactive element disintegrates for an interval of time equal to its mean lifetime. The fraction that has disintegrated is ______
The half-life of the radioactive substance is 40 days. The substance will disintegrate completely in
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
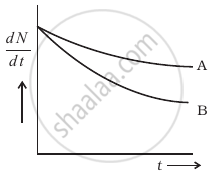
Which sample, A or B shown in figure has shorter mean-life?