Advertisements
Advertisements
प्रश्न
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
उत्तर
Let the number of atoms present at t = 0 be N0.
Let N be the number of radio-active isotopes present at time t.
Then,
N = N0e−λt
Here, `lambda` = Disintegration constant
∴ Number of radioactive isotopes decayed = `N_0 - N = N_0 - N_0e^(-lambdat)`
= `N_0(1-e^(-lambdat))` ...(1)
Rate of decay (R) is given by
`R = lambdaN_0` ...(2)
Substituting the value of `N_0` from equation (2) to equation (1), we get
`N = N_0(1-e^(-lambdat))`
= `R/lambda (1 - e^(-lambdat))`
APPEARS IN
संबंधित प्रश्न
The Q value of a nuclear reaction A + b → C + d is defined by
Q = [mA+ mb − mC − md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^12_6C + ^12_6C ->^20_10Ne + ^4_2He}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12C)` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
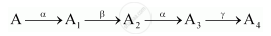
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
The radioactive isotope D decays according to the sequence
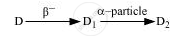
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Define the term 'decay constant' of a radioactive sample. The rate of disintegration of a given radioactive nucleus is 10000 disintegrations/s and 5,000 disintegrations/s after 20 hr. and 30 hr. respectively from start. Calculate the half-life and the initial number of nuclei at t= 0.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
What percentage of radioactive substance is left after five half-lives?
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
The half-life of the radioactive substance is 40 days. The substance will disintegrate completely in
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
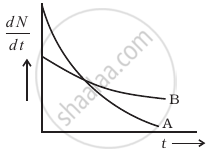
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
Which sample, A or B shown in figure has shorter mean-life?
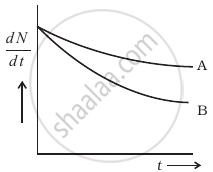
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
