Advertisements
Advertisements
प्रश्न
Obtain the relation between the decay constant and half life of a radioactive sample.
उत्तर
The number of atoms at any instant in a radioactive sample is given by
N=N0e−λt
where
N=total number of atoms at any instant
N0=number of atoms in radioactive substance at t=0
λ=decay constant
t=time
When t=T (Where T is the half life of the sample)
`N=N_0/2`
`=>N_0/2=N_0e^(-lambdat)`
`=1/2=e^(-lambdaT)`
`=>e^(lambdaT)=2`
Taking log on both the sides, we get
`lambdaT=log_e2=2.303 lod_10 2`
`=>T=(2.303 lod_10 2)/lambda`
`=>T=(2.303 xx 0.3010)/lambda`
`=>T=0.6931/lambda`
Thus, half life of a radioactive substance is inversely propotional to decay constant.
APPEARS IN
संबंधित प्रश्न
Why is it found experimentally difficult to detect neutrinos in nuclear β-decay?
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
The radioactive isotope D decays according to the sequence
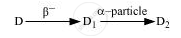
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
A source contains two species of phosphorous nuclei, \[\ce{_15^32P}\] (T1/2 = 14.3 d) and \[\ce{_15^33P}\] (T1/2 = 25.3 d). At time t = 0, 90% of the decays are from \[\ce{_15^32P}\]. How much time has to elapse for only 15% of the decays to be from \[\ce{_15^32P}\]?
What percentage of radioactive substance is left after five half-lives?
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
The half-life of `""_82^210Pb` is 22.3 y. How long will it take for its activity 0 30% of the initial activity?
