Advertisements
Advertisements
प्रश्न
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
उत्तर
Activity for a radioactive substance is given as
\[A = \frac{d N}{d t} = \lambda N = \frac{0 . 693N}{T}\]
\[ \therefore A_1 = \frac{0 . 693 N_1}{T_1}; A_2 = \frac{0 . 693 N_2}{T_2}\]
\[ \Rightarrow \frac{A_1}{A_2} = \frac{N_1}{T_1} \times \frac{T_2}{N_2}\]
\[ \Rightarrow \frac{A_1}{A_2} = \frac{N_1}{N_2} \times \frac{T_2}{T_1}\]
APPEARS IN
संबंधित प्रश्न
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
How is the mean life of a given radioactive nucleus related to the decay constant?
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
Two electrons are ejected in opposite directions from radioactive atoms in a sample of radioactive material. Let c denote the speed of light. Each electron has a speed of 0.67 c as measured by an observer in the laboratory. Their relative velocity is given by ______.
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
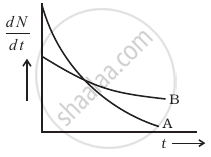
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
Draw a graph showing the variation of decay rate with number of active nuclei.
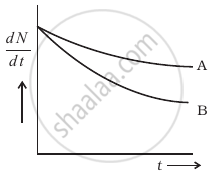
Which sample, A or B shown in figure has shorter mean-life?
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
The activity R of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:
| t (h) | 0 | 1 | 2 | 3 | 4 |
| R (MBq) | 100 | 35.36 | 12.51 | 4.42 | 1.56 |
- Plot the graph of R versus t and calculate the half-life from the graph.
- Plot the graph of ln `(R/R_0)` versus t and obtain the value of half-life from the graph.
