Advertisements
Advertisements
प्रश्न
The activity R of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:
| t (h) | 0 | 1 | 2 | 3 | 4 |
| R (MBq) | 100 | 35.36 | 12.51 | 4.42 | 1.56 |
- Plot the graph of R versus t and calculate the half-life from the graph.
- Plot the graph of ln `(R/R_0)` versus t and obtain the value of half-life from the graph.
Advertisements
उत्तर
We have listed R(MBq) and In `(R/R_0)` in the table below.
| t (h) | 0 | 1 | 2 | 3 | 4 |
| R (MBq) | 100 | 35.36 | 12.51 | 4.42 | 1.56 |
| `R/R_0` | – | – 1.04 | – 2.08 | – 3.11 | – 4.16 |
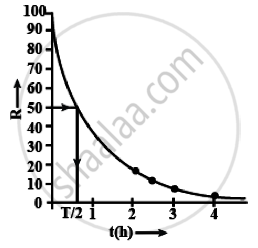
i. Graph between R versus t is an exponential curve. From the graph at slightly more than `t = 1/2 h` the R should be 50% so at R = 50% the t(h) = 0.7h
= 0.7 × 60 min
= 42 min
ii. The adjacent figure shows the graph of In `(R/R_0)` versus t.
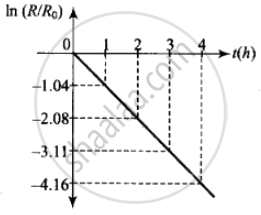
The slope of this graph = – λ
From the graph,
`λ = - ((-4.16 - 3.11)/1) = 1.05 h^-1`
Hence half-life `T_(1/2) = 0.693/λ = 0.693/1.05` = 0.66 h
= 39.6 min ≈ 40 min
APPEARS IN
संबंधित प्रश्न
Obtain the relation between the decay constant and half life of a radioactive sample.
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive `""_6^14"C"` present with the stable carbon isotope `""_6^12"C"`. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of `""_6^14"C"` and the measured activity, the age of the specimen can be approximately estimated. This is the principle of `""_6^14"C"` dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
Why is it experimentally found difficult to detect neutrinos in this process ?
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
The radioactive isotope D decays according to the sequence
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
A radioactive isotope is being produced at a constant rate dN/dt = R in an experiment. The isotope has a half-life t1/2. Show that after a time t >> t1/2 the number of active nuclei will become constant. Find the value of this constant.
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
What percentage of radioactive substance is left after five half-lives?
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
The half-life of `""_82^210Pb` is 22.3 y. How long will it take for its activity 0 30% of the initial activity?
