Advertisements
Advertisements
प्रश्न
A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value?
A radioactive isotope has a half-life of 10 years. How long will it take for the activity to reduce to 3.125% ?
उत्तर १
Half-life of the radioactive isotope = T years
Original amount of the radioactive isotope = N0
a) After decay, the amount of the radioactive isotope = N
It is given that only 3.125% of N0 remains after decay. Hence, we can write
`"N"/"N"_0` = 3.125% = `3.125/100 = 1/32`
But `"N"/"N"_0 = "e"^(-lambda"t")`
Where,
λ = Decay constant
t = Time
∴ `-lambda"t" = 1/32`
`-lambda"t" =ln 1 - ln32`
`-lambda"t" = 0 - 3.4657`
`"t" = 3.4657/lambda`
Since `lambda = 0.693/"T"`
∴ `"t" = 3.466/(0.693/"T") ≈ 5"T years"`
Hence, the isotope will take about 5T years to reduce to 3.125% of its original value.
b) After decay, the amount of the radioactive isotope = N
It is given that only 1% of N0 remains after decay. Hence, we can write:
`"N"/"N"_0` = 1% = `1/100`
But `"N"/"N"_0 = "e"^(-lambda"t")`
∴ `"e"^(-lambda"t") = 1/100`
`-lambda"t" = ln 1 - ln 100`
`"t" = 4.6052/lambda`
Since `lambda = 0.693/"T"`
∴ `t = 4.6052/(0.693/"T") = 6.645 "T years"`
Hence, the isotope will take about 6.645T years to reduce to 1% of its original value.
उत्तर २
`A_0 = 100`
`A_1 = 3.125`
`A_t = A_0.e^(-lambdat)`
`3.125 = 100e^(-0.693/10) t`
`3.125/100 = e^(-0.0693 t)`
`100/3.125 = e^(0.0693t)`
`log_e 100/3.125 = 0.0693t`
`t_2 = (2.303log_10^32)/0.0693`
t = 50.1 year
APPEARS IN
संबंधित प्रश्न
State the law of radioactive decay.
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive `""_6^14"C"` present with the stable carbon isotope `""_6^12"C"`. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of `""_6^14"C"` and the measured activity, the age of the specimen can be approximately estimated. This is the principle of `""_6^14"C"` dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
The Q value of a nuclear reaction \[\ce{A + b → C + d}\] is defined by
Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12"C")` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
The Q value of a nuclear reaction A + b → C + d is defined by
Q = [mA+ mb − mC − md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^12_6C + ^12_6C ->^20_10Ne + ^4_2He}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12C)` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
A radioactive nucleus 'A' undergoes a series of decays as given below:
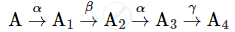
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
Define 'activity' of a radioactive substance ?
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of 14C averaged about 0.255 Bq per gram of carbon.
(a) What fraction of carbon atoms were 14C?
(b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? The half-life of 14C is 5730 years.
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom ______.
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
The radioactivity of an old sample of whisky due to tritium (half-life 12.5 years) was found to be only about 4% of that measured in a recently purchased bottle marked 10 years old. The age of a sample is ______ years.
