Advertisements
Advertisements
प्रश्न
The Q value of a nuclear reaction \[\ce{A + b → C + d}\] is defined by
Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12"C")` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
उत्तर
The given nuclear reaction is:
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
It is given that:
Atomic mass `m(""_1^1"H")` = 1.007825 u
Atomic mass `m(""_1^3"H")` = 3.016049 u
Atomic mass `m(""_1^2"H") = 2.014102 u`
According to the question, the Q-value of the reaction can be written as:
Q = `["m"(""_1^1"H") + "m"(""_1^3"H") - 2"m"(""_1^2"H")]"c"^2`
Q = (- 0.00433 c2)u
But 1 u = 931.5 MeV/c2
`= [1.007825 + 3.016049 - 2 xx 2.014102]c^2`
`"Q" = - 0.00433 xx 931.5 = - 4.0334` MeV
The negative Q-value of the reaction shows that the reaction is endothermic.
APPEARS IN
संबंधित प्रश्न
The decay constant of radioactive substance is 4.33 x 10-4 per year. Calculate its half life period.
Why is it experimentally found difficult to detect neutrinos in this process ?
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
28Th emits an alpha particle to reduce to 224Ra. Calculate the kinetic energy of the alpha particle emitted in the following decay:
`""^228"Th" → ""^224"Ra"^(∗) + alpha`
`""^224"Ra"^(∗) → ""^224"Ra" + γ (217 "keV")`.
Atomic mass of 228Th is 228.028726 u, that of 224Ra is 224.020196 u and that of `""_2^4H` is 4.00260 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
The isotope \[\ce{^57Co}\] decays by electron capture to \[\ce{^57Fe}\] with a half-life of 272 d. The \[\ce{^57Fe}\] nucleus is produced in an excited state, and it almost instantaneously emits gamma rays.
(a) Find the mean lifetime and decay constant for 57Co.
(b) If the activity of a radiation source 57Co is 2.0 µCi now, how many 57Co nuclei does the source contain?
c) What will be the activity after one year?
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of 14C averaged about 0.255 Bq per gram of carbon.
(a) What fraction of carbon atoms were 14C?
(b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? The half-life of 14C is 5730 years.
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
What percentage of radioactive substance is left after five half-lives?
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
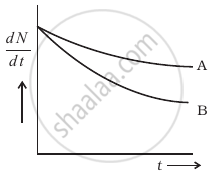
Which sample, A or B shown in figure has shorter mean-life?
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
