Advertisements
Advertisements
Questions
A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value?
A radioactive isotope has a half-life of 10 years. How long will it take for the activity to reduce to 3.125% ?
Solution 1
Half-life of the radioactive isotope = T years
Original amount of the radioactive isotope = N0
a) After decay, the amount of the radioactive isotope = N
It is given that only 3.125% of N0 remains after decay. Hence, we can write
`"N"/"N"_0` = 3.125% = `3.125/100 = 1/32`
But `"N"/"N"_0 = "e"^(-lambda"t")`
Where,
λ = Decay constant
t = Time
∴ `-lambda"t" = 1/32`
`-lambda"t" =ln 1 - ln32`
`-lambda"t" = 0 - 3.4657`
`"t" = 3.4657/lambda`
Since `lambda = 0.693/"T"`
∴ `"t" = 3.466/(0.693/"T") ≈ 5"T years"`
Hence, the isotope will take about 5T years to reduce to 3.125% of its original value.
b) After decay, the amount of the radioactive isotope = N
It is given that only 1% of N0 remains after decay. Hence, we can write:
`"N"/"N"_0` = 1% = `1/100`
But `"N"/"N"_0 = "e"^(-lambda"t")`
∴ `"e"^(-lambda"t") = 1/100`
`-lambda"t" = ln 1 - ln 100`
`"t" = 4.6052/lambda`
Since `lambda = 0.693/"T"`
∴ `t = 4.6052/(0.693/"T") = 6.645 "T years"`
Hence, the isotope will take about 6.645T years to reduce to 1% of its original value.
Solution 2
`A_0 = 100`
`A_1 = 3.125`
`A_t = A_0.e^(-lambdat)`
`3.125 = 100e^(-0.693/10) t`
`3.125/100 = e^(-0.0693 t)`
`100/3.125 = e^(0.0693t)`
`log_e 100/3.125 = 0.0693t`
`t_2 = (2.303log_10^32)/0.0693`
t = 50.1 year
APPEARS IN
RELATED QUESTIONS
The decay constant of radioactive substance is 4.33 x 10-4 per year. Calculate its half life period.
How is the mean life of a given radioactive nucleus related to the decay constant?
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
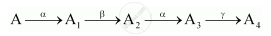
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
28Th emits an alpha particle to reduce to 224Ra. Calculate the kinetic energy of the alpha particle emitted in the following decay:
`""^228"Th" → ""^224"Ra"^(∗) + alpha`
`""^224"Ra"^(∗) → ""^224"Ra" + γ (217 "keV")`.
Atomic mass of 228Th is 228.028726 u, that of 224Ra is 224.020196 u and that of `""_2^4H` is 4.00260 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of `""_80^197`Hg (electron capture to `""_79^197`Au) is 1.8 × 10−4 S−1. (a) What is the half-life? (b) What is the average-life? (c) How much time will it take to convert 25% of this isotope of mercury into gold?
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
A radioactive isotope is being produced at a constant rate dN/dt = R in an experiment. The isotope has a half-life t1/2. Show that after a time t >> t1/2 the number of active nuclei will become constant. Find the value of this constant.
A source contains two species of phosphorous nuclei, \[\ce{_15^32P}\] (T1/2 = 14.3 d) and \[\ce{_15^33P}\] (T1/2 = 25.3 d). At time t = 0, 90% of the decays are from \[\ce{_15^32P}\]. How much time has to elapse for only 15% of the decays to be from \[\ce{_15^32P}\]?
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
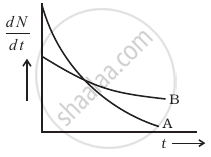
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
