Advertisements
Advertisements
Question
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive `""_6^14"C"` present with the stable carbon isotope `""_6^12"C"`. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of `""_6^14"C"` and the measured activity, the age of the specimen can be approximately estimated. This is the principle of `""_6^14"C"` dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
Solution
Decay rate of living carbon-containing matter, R = 15 decay/min
Let N be the number of radioactive atoms present in a normal carbon-containing matter.
Half-life of `""_6^14"C"`, `"T"_(1/2)` = 5730 years
The decay rate of the specimen obtained from the Mohenjodaro site:
R' = 9 decays/min
Let N' be the number of radioactive atoms present in the specimen during the Mohenjodaro period.
Therefore, we can relate the decay constant, λ and time, t as:
`"N"/"N'" = "R"/"R'" = "e"^(-lambda"t")`
`"e"^(-lambda"t") = 9/15 = 3/5`
`-lambda"t" = log_"e" 3/5 = -0.5108`
∴ `"t" = 0.5108/lambda`
But `lambda = 0.639/"T"_"1/2" = 0.693/5730`
∴ t = `0.5108/(0.693/5730)`
= 4223.5 years
Hence, the approximate age of the Indus-Valley civilisation is 4223.5 years.
APPEARS IN
RELATED QUESTIONS
(a) Write the basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus.
(b) In the reactions given below:
(i)`""_16^11C->_y^zB+x+v`
(ii)`""_6^12C+_6^12C->_a^20 Ne + _b^c He`
Find the values of x, y, and z and a, b and c.
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value?
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
The masses of 11C and 11B are respectively 11.0114 u and 11.0093 u. Find the maximum energy a positron can have in the β*-decay of 11C to 11B.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
Identify the nature of the radioactive radiations emitted in each step of the decay process given below.
`""_Z^A X -> _Z^A _-1^-4 Y ->_Z^A _-1^-4 W`
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
'Half-life' of a radioactive substance accounts for ______.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
Two electrons are ejected in opposite directions from radioactive atoms in a sample of radioactive material. Let c denote the speed of light. Each electron has a speed of 0.67 c as measured by an observer in the laboratory. Their relative velocity is given by ______.
The half-life of the radioactive substance is 40 days. The substance will disintegrate completely in
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
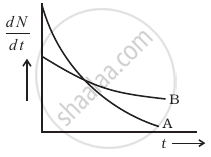
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
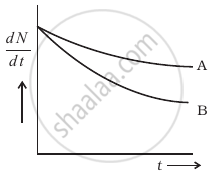
Which sample, A or B shown in figure has shorter mean-life?
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
