Advertisements
Advertisements
Question
Write nuclear reaction equation for electron capture of `""_54^120"Xe"`.
Solution
α is a nucleus of helium `(""_2^4"He")` and β is an electron (e− for β− and e+ for β+). In every α-decay, there is a loss of 2 protons and 4 neutrons. In every β+-decay, there is a loss of 1 proton and a neutrino is emitted from the nucleus. In every β−-decay, there is a gain of 1 proton and an antineutrino is emitted from the nucleus.
For the given case, the various nuclear reaction can be written as:
`""_54^120"Xe" + "e"^+ -> _53^120"I" + "v"`
APPEARS IN
RELATED QUESTIONS
The half life of a certain radioactive material against \u0003α-decay is 100 days. After how much time, will the undecayed fraction of the material be 6.25%?
Write nuclear reaction equation for α-decay of `""_88^226"Ra"`.
Write nuclear reaction equation for β−-decay of `""_83^210"Bi"`.
Write nuclear reaction equation for β+-decay of `""_6^11"C"`.
Draw graphs showing variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
A radioactive nucleus has a decay constant λ = 0.3465 (day)–1. How long would it take the nucleus to decay to 75% of its initial amount?
Plot a graph showing variation of activity of a given radioactive sample with time.
The sequence of stepwise decay of a radioactive nucleus is
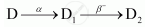
If the atomic number and mass number of D2 are 71 and 176 respectively, what are their corresponding values of D?
The half-life of 199Au is 2.7 days. (a) Find the activity of a sample containing 1.00 µg of 198Au. (b) What will be the activity after 7 days? Take the atomic weight of 198Au to be 198 g mol−1.
Radioactive 131I has a half-life of 8.0 days. A sample containing 131I has activity 20 µCi at t = 0. (a) What is its activity at t = 4 days? (b) What is its decay constant at t = 4.0 days?
A certain sample of a radioactive material decays at the rate of 500 per second at a certain time. The count rate falls to 200 per second after 50 minutes. (a) What is the decay constant of the sample? (b) What is its half-life?
The count rate from a radioactive sample falls from 4.0 × 106 per second to 1.0 × 106per second in 20 hours. What will be the count rate 100 hours after the beginning?
`""_83^212"Bi"` can disintegrate either by emitting an α-particle of by emitting a β−-particle. (a) Write the two equations showing the products of the decays. (b) The probabilities of disintegration α-and β-decays are in the ratio 7/13. The overall half-life of 212Bi is one hour. If 1 g of pure 212Bi is taken at 12.00 noon, what will be the composition of this sample at 1 P.m. the same day?
A sample contains a mixture of 108Ag and 110Ag isotopes each having an activity of 8.0 × 108 disintegration per second. 110Ag is known to have larger half-life than 108Ag. The activity A is measured as a function of time and the following data are obtained.
| Time (s) |
Activity (A) (108 disinte- grations s−1) |
Time (s) |
Activity (A 108 disinte-grations s−1) |
| 20 40 60 80 100 |
11.799 9.1680 7.4492 6.2684 5.4115 |
200 300 400 500 |
3.0828 1.8899 1.1671 0.7212 |
(a) Plot ln (A/A0) versus time. (b) See that for large values of time, the plot is nearly linear. Deduce the half-life of 110Ag from this portion of the plot. (c) Use the half-life of 110Ag to calculate the activity corresponding to 108Ag in the first 50 s. (d) Plot In (A/A0) versus time for 108Ag for the first 50 s. (e) Find the half-life of 108Ag.
Complete the following nuclear reactions :
(i) `"_15^32P -> ` `"_z^AX + bar(e) + bar(v)`
(ii) `"_6^12 C `+`"_6^12C ->` ` "_2^A Y + ` `"_4^2 He`
A radioactive substance decays to 1/16th of its initial mass in 40 days. The half-life of the substance, in days, is:
Half-life of a certain radioactive material is 8 hours.
Find the disintegration constant of this material.
