Advertisements
Advertisements
Question
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
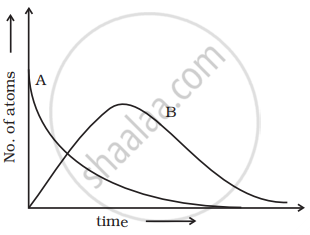
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
Solution
Consider radioactive nucleus A have N0 atoms of A initially; or at t = 0, NA = N0 (maximum) whole NB = 0. As time increases, NA decreases exponentially and the number of atoms of B increases. After some time NB becomes maximum. As B is an intermediate nuclei which is also radioactive, it also starts decaying and finally drops to zero exponentially by radioactive decay law. We can represent the situation as shown in the graph.
APPEARS IN
RELATED QUESTIONS
Obtain the relation between the decay constant and half life of a radioactive sample.
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
Define the activity of a given radioactive substance. Write its S.I. unit.
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
Two electrons are ejected in opposite directions from radioactive atoms in a sample of radioactive material. Let c denote the speed of light. Each electron has a speed of 0.67 c as measured by an observer in the laboratory. Their relative velocity is given by ______.
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
