Advertisements
Advertisements
प्रश्न
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
उत्तर
Take a `""_6^14"C"` emission nuclear reaction:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
We know that:
Mass of `""_88^223"Ra"` m1 = 223.01850 u
Mass of `""_82^209"Pb"` m2 = 208.98107 u
Mass of `""_6^14"C"`, m3 = 14.00324 u
Hence, the Q-value of the reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 208.98107 − 14.00324) c2
= (0.03419 c2) u
But 1 u = 931.5 MeV/c2
∴ Q = 0.03419 × 931.5
= 31.848 MeV
Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed.
Now take a `""_2^4"He"` emission nuclear reaction:
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
We know that:
Mass of `""_88^223"Ra"`, m1 = 223.01850
Mass of `""_82^219"Rn"` m2 = 219.00948
Mass of `""_2^4"He"`, m3 = 4.00260
Q-value of this nuclear reaction is given as:
Q = (m1 − m2 − m3) c2
= (223.01850 − 219.00948 − 4.00260) C2
= (0.00642 c2) u
= 0.00642 × 931.5 = 5.98 MeV
Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed.
APPEARS IN
संबंधित प्रश्न
How is the mean life of a given radioactive nucleus related to the decay constant?
Obtain the relation between the decay constant and half life of a radioactive sample.
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
The Q value of a nuclear reaction \[\ce{A + b → C + d}\] is defined by
Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12"C")` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
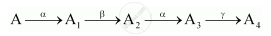
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
The radioactive isotope D decays according to the sequence
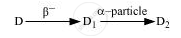
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
Lithium (Z = 3) has two stable isotopes 6Li and 7Li. When neutrons are bombarded on lithium sample, electrons and α-particles are ejected. Write down the nuclear process taking place.
Define the term 'decay constant' of a radioactive sample. The rate of disintegration of a given radioactive nucleus is 10000 disintegrations/s and 5,000 disintegrations/s after 20 hr. and 30 hr. respectively from start. Calculate the half-life and the initial number of nuclei at t= 0.
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
What is the amount of \[\ce{_27^60Co}\] necessary to provide a radioactive source of strength 10.0 mCi, its half-life being 5.3 years?
The isotope \[\ce{^57Co}\] decays by electron capture to \[\ce{^57Fe}\] with a half-life of 272 d. The \[\ce{^57Fe}\] nucleus is produced in an excited state, and it almost instantaneously emits gamma rays.
(a) Find the mean lifetime and decay constant for 57Co.
(b) If the activity of a radiation source 57Co is 2.0 µCi now, how many 57Co nuclei does the source contain?
c) What will be the activity after one year?
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
'Half-life' of a radioactive substance accounts for ______.
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
Draw a graph showing the variation of decay rate with number of active nuclei.
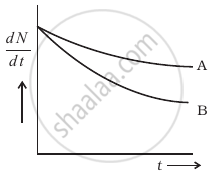
Which sample, A or B shown in figure has shorter mean-life?
The half-life of `""_82^210Pb` is 22.3 y. How long will it take for its activity 0 30% of the initial activity?
