Advertisements
Advertisements
प्रश्न
How is the mean life of a given radioactive nucleus related to the decay constant?
उत्तर
To find the mean life t1, we need to use the equation of radioactive law.
The number of nuclei which decay in the time interval t to t + Δt is R(t)Δt (= λN0 e–λt Δt). Each of them has lived for time t.
Thus, the total life of all these nuclei would be t λN0 e–λt Δt. It is clear that some nuclei may live for a short time, while others may live longer. Therefore, to obtain the mean life, we have to integrate the above expression over all times from 0 to ∞ and divide it by the total number N0 of nuclei at t = 0.
Therefore, we get
`t=(lambdaN_0int_0^oote^(-lambdat)dt)/N_0=lambdaint_0^oote^(-lambdat)dt`
Solving by integration-by-parts we get
`t=lambdaxx1/lambda^2=1/lambda`
APPEARS IN
संबंधित प्रश्न
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
'Half-life' of a radioactive substance accounts for ______.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
What percentage of radioactive substance is left after five half-lives?
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
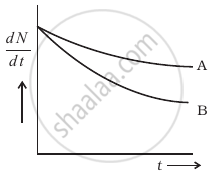
Which sample, A or B shown in figure has shorter mean-life?
The activity R of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:
| t (h) | 0 | 1 | 2 | 3 | 4 |
| R (MBq) | 100 | 35.36 | 12.51 | 4.42 | 1.56 |
- Plot the graph of R versus t and calculate the half-life from the graph.
- Plot the graph of ln `(R/R_0)` versus t and obtain the value of half-life from the graph.
