Advertisements
Advertisements
Question
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
Solution
Given:
Decay constant, `lambda = 4.9 xx 10^-18 "s"^-1`
(a) Average life of uranium (`tau`) is given by
`tau = 1/lambda`
= `1/(4.9 xx 10^-18)`
= `1/4.9 xx 10^18 "s"`
= `10^16/(4.9 xx 365 xx 24 xx 36) "years"`
= `10^16/(4.9 xx 365 xx 24 xx 36) "years"`
= `6.47 xx 10^-7 xx 10^16 "years"`
= `6.47 xx 10^9 "years"`
(b) Half-life of uranium (`T_"1/2"`) is given by
`T_"1/2" = 0.693/lambda = 0.693/(4.9 xx 10^-18)`
= `0.693/4.9 xx 10^18 "s"`
= `0.1414 xx 10^18 "s"`
= `(0.1414 xx 10^18)/(365 xx 24 xx 3600)`
= `(1414 xx 10^12)/(365 xx 24 xx 36)`
= `4.48 xx 10^-3 xx 10^12`
= `4.5 xx 10^9` years
(c) Time, t = 9 × 109 years
Activity (A) of the sample, at any time t, is given by
`A = A_0/2^(t/T_"1/2")`
Here , `A_0` = Activity of the sample at t = 0
`therefore A_0/A = 2^((9 xx 10^9)/(4.5 xx 10^9)) = 2^2 = 4`
APPEARS IN
RELATED QUESTIONS
The decay constant of radioactive substance is 4.33 x 10-4 per year. Calculate its half life period.
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
The radioactive isotope D decays according to the sequence
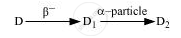
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
Calculate the maximum kinetic energy of the beta particle emitted in the following decay scheme:
12N → 12C* + e+ + v
12C* → 12C + γ (4.43MeV).
The atomic mass of 12N is 12.018613 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Define the term 'decay constant' of a radioactive sample. The rate of disintegration of a given radioactive nucleus is 10000 disintegrations/s and 5,000 disintegrations/s after 20 hr. and 30 hr. respectively from start. Calculate the half-life and the initial number of nuclei at t= 0.
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
A radioactive element disintegrates for an interval of time equal to its mean lifetime. The fraction that has disintegrated is ______
Which one of the following nuclei has shorter meant life?
'Half-life' of a radioactive substance accounts for ______.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
