Advertisements
Advertisements
Question
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Solution
At t = T1/2 (half life ), N = `(N_0)/2`
Putting this, into
N = N0e-λt [where λ = decay constant]
We get `1/2 = e^(-lambdaT_(1/2)`
⇒ `1/2 = 1/(e^(lambdaT_(1/2))) ⇒ e^(lambdaT_(1/2)) = 2`
` e^(lambdaT_(1/2)) = 2`
Taking logarithm to both sides,
`lambdaT_(1/2) = "log "e^2`
∴ `T_(1/2) = ("log "e^2)/lambda`
i.e., `T_(1/2) = (2.303 xx "log"10^2)/lambda`
`T_(1/2) = (2.3 xx0.301)/lambda`
∴ `T_(1/2) =0.692/lambda`
APPEARS IN
RELATED QUESTIONS
Why is it found experimentally difficult to detect neutrinos in nuclear β-decay?
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
Define 'activity' of a radioactive substance ?
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
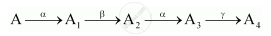
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
'Half-life' of a radioactive substance accounts for ______.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
