Advertisements
Advertisements
Question
Define the term 'decay constant' of a radioactive sample. The rate of disintegration of a given radioactive nucleus is 10000 disintegrations/s and 5,000 disintegrations/s after 20 hr. and 30 hr. respectively from start. Calculate the half-life and the initial number of nuclei at t= 0.
Solution
The decay constant is the fraction of the number of atoms that decay in one second.
It is denoted by A.
Let N0 be the initial number of nuclei,
Let λ be the decay constant
Let t1/2 be the half-life
The instantaneous activity of radioactive material is given by `A = A_0e^(-lambdat)`
Where A0 is activity at t = 0
Therefore, after 20 hours is 10,000 disintegrations per second
`10,000 = A_0e^(-lambda(20 xx 3600))` ...(1)
Activity after 30 hours is 5,000 disintegrations per second
`5000 = A_0e^(-lambda(30 xx 3600))` ..(2)
On dividing (1) by (2),
`2 = e^(lambda xx 3600)`
⇒ `lambda = ln 2/36000 = 1.92 xx 10^-5`
And half life is,
`ln 2/(1.92 xx 10^-5) = 36,000"s" = 10` hours
Since,
`(dN)/(dt) = lambdaN`
`1000 = (1.92 xx 10^-5) xx N_1`
⇒ `N_1 = (10,000)/(1.92 xx 10^-5) = 5.208 xx 10^8`
Therefore, the half life is 10 hours, thus the initial number of nuclei is `N_0 = 10.416 xx 10^8`
APPEARS IN
RELATED QUESTIONS
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
Why is it experimentally found difficult to detect neutrinos in this process ?
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of 14C averaged about 0.255 Bq per gram of carbon.
(a) What fraction of carbon atoms were 14C?
(b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? The half-life of 14C is 5730 years.
'Half-life' of a radioactive substance accounts for ______.
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
What percentage of radioactive substance is left after five half-lives?
The variation of decay rate of two radioactive samples A and B with time is shown in figure.
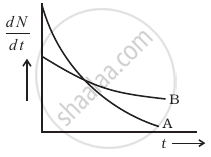
Which of the following statements are true?
- Decay constant of A is greater than that of B, hence A always decays faster than B.
- Decay constant of B is greater than that of A but its decay rate is always smaller than that of A.
- Decay constant of A is greater than that of B but it does not always decay faster than B.
- Decay constant of B is smaller than that of A but still its decay rate becomes equal to that of A at a later instant.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
