Advertisements
Advertisements
Question
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
Solution
Half life of `""_38^90"Sr", "t"_(1/2)`= 28 years
= 28 × 365 × 24 × 60 × 60
= 8.83 × 108 s
Mass of the isotope, m = 15 mg
90 g of `""_38^90"Sr"` atom contains 6.023 × 1023 (Avogadro’s number) atoms.
Therefore, 15 mg of `""_38^90"Sr"` contains:
`(6.023 xx 10^23 xx 15 xx 10^(-3))/90 "i.e." 1.0038 xx 10^20` number of atoms
Rate of disintegration, `"dN"/"dt" = lambda"N"`
Where,
λ = Decay constant = `0.693/(8.83 xx 10^8) "s"^(-1)`
`= "dN"/"dt" = (0.693 xx 1.0038 xx 10^20)/(8.83 xx 10^8) = 7.878 xx 10^10 "atoms/s"`
Hence, the disintegration rate of 15 mg of the given isotope is 7.878 × 1010 atoms/s.
APPEARS IN
RELATED QUESTIONS
(a) Write the basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus.
(b) In the reactions given below:
(i)`""_16^11C->_y^zB+x+v`
(ii)`""_6^12C+_6^12C->_a^20 Ne + _b^c He`
Find the values of x, y, and z and a, b and c.
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
A radioactive nucleus 'A' undergoes a series of decays as given below:
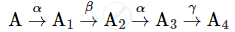
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
(a) Derive the relation between the decay constant and half life of a radioactive substance.
(b) A radioactive element reduces to 25% of its initial mass in 1000 years. Find its half life.
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
Why is it experimentally found difficult to detect neutrinos in this process ?
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
The radioactive isotope D decays according to the sequence
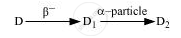
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
When charcoal is prepared from a living tree, it shows a disintegration rate of 15.3 disintegrations of 14C per gram per minute. A sample from an ancient piece of charcoal shows 14C activity to be 12.3 disintegrations per gram per minute. How old is this sample? Half-life of 14C is 5730 y.
A radioactive isotope is being produced at a constant rate dN/dt = R in an experiment. The isotope has a half-life t1/2. Show that after a time t >> t1/2 the number of active nuclei will become constant. Find the value of this constant.
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Identify the nature of the radioactive radiations emitted in each step of the decay process given below.
`""_Z^A X -> _Z^A _-1^-4 Y ->_Z^A _-1^-4 W`
A source contains two species of phosphorous nuclei, \[\ce{_15^32P}\] (T1/2 = 14.3 d) and \[\ce{_15^33P}\] (T1/2 = 25.3 d). At time t = 0, 90% of the decays are from \[\ce{_15^32P}\]. How much time has to elapse for only 15% of the decays to be from \[\ce{_15^32P}\]?
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half life of 1 year. After 1 year ______.
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
