Advertisements
Advertisements
प्रश्न
State the law of radioactive decay.
उत्तर
Law of radioactive decay:
The number of nuclei undergoing the decay per unit time is proportional to the number of unchanged nuclei present at that instant.
If ‘N’ is the number of nuclei present at any instant ‘t’, ‘dN’ is the number of nuclei that disintegrated in short interval of time ‘dt’, then according to decay law,
`- (dN)/dt ∝ N`
`:.(dN)/dt = -lambda N`
where, `lambda` is known as decay constant or disintegration constant. The negative sign indicates disintegration of atoms.
APPEARS IN
संबंधित प्रश्न
The decay constant of radioactive substance is 4.33 x 10-4 per year. Calculate its half life period.
(a) Write the basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus.
(b) In the reactions given below:
(i)`""_16^11C->_y^zB+x+v`
(ii)`""_6^12C+_6^12C->_a^20 Ne + _b^c He`
Find the values of x, y, and z and a, b and c.
How is the mean life of a given radioactive nucleus related to the decay constant?
Write symbolically the process expressing the β+ decay of `""_11^22Na`. Also write the basic nuclear process underlying this decay.
Obtain the amount of `""_27^60"Co"` necessary to provide a radioactive source of 8.0 mCi strength. The half-life of `""_27^60"Co"` is 5.3 years.
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
The Q value of a nuclear reaction \[\ce{A + b → C + d}\] is defined by
Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^1_1H + ^3_1H -> ^2_1H + ^2_1H}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12"C")` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
Represent Radioactive Decay curve using relation `N = N_o e^(-lambdat)` graphically
A radioactive nucleus 'A' undergoes a series of decays as given below:
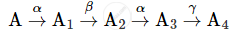
The mass number and atomic number of A2 are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.
Using the equation `N = N_0e^(-lambdat)` obtain the relation between half-life (T) and decay constant (`lambda`) of a radioactive substance.
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
Define the activity of a given radioactive substance. Write its S.I. unit.
In a given sample, two radioisotopes, A and B, are initially present in the ration of 1 : 4. The half lives of A and B are respectively 100 years and 50 years. Find the time after which the amounts of A and B become equal.
The radioactive isotope D decays according to the sequence
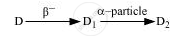
If the mass number and atomic number of D2 are 176 and 71 respectively, what is (i) the mass number (ii) atomic number of D?
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
Calculate the maximum kinetic energy of the beta particle emitted in the following decay scheme:
12N → 12C* + e+ + v
12C* → 12C + γ (4.43MeV).
The atomic mass of 12N is 12.018613 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of `""_80^197`Hg (electron capture to `""_79^197`Au) is 1.8 × 10−4 S−1. (a) What is the half-life? (b) What is the average-life? (c) How much time will it take to convert 25% of this isotope of mercury into gold?
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
A radioactive isotope is being produced at a constant rate dN/dt = R in an experiment. The isotope has a half-life t1/2. Show that after a time t >> t1/2 the number of active nuclei will become constant. Find the value of this constant.
The half-life of 40K is 1.30 × 109 y. A sample of 1.00 g of pure KCI gives 160 counts s−1. Calculate the relative abundance of 40K (fraction of 40K present) in natural potassium.
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Define one Becquerel.
A radioactive substance disintegrates into two types of daughter nuclei, one type with disintegration constant λ1 and the other type with disintegration constant λ2 . Determine the half-life of the radioactive substance.
The isotope \[\ce{^57Co}\] decays by electron capture to \[\ce{^57Fe}\] with a half-life of 272 d. The \[\ce{^57Fe}\] nucleus is produced in an excited state, and it almost instantaneously emits gamma rays.
(a) Find the mean lifetime and decay constant for 57Co.
(b) If the activity of a radiation source 57Co is 2.0 µCi now, how many 57Co nuclei does the source contain?
c) What will be the activity after one year?
Before the year 1900 the activity per unit mass of atmospheric carbon due to the presence of 14C averaged about 0.255 Bq per gram of carbon.
(a) What fraction of carbon atoms were 14C?
(b) An archaeological specimen containing 500 mg of carbon, shows 174 decays in one hour. What is the age of the specimen, assuming that its activity per unit mass of carbon when the specimen died was equal to the average value of the air? The half-life of 14C is 5730 years.
Two radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2 will belie after a time.
A radioactive element disintegrates for an interval of time equal to its mean lifetime. The fraction that has disintegrated is ______
Which one of the following nuclei has shorter meant life?
The half-life of a radioactive sample undergoing `alpha` - decay is 1.4 x 1017 s. If the number of nuclei in the sample is 2.0 x 1021, the activity of the sample is nearly ____________.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
What percentage of radioactive substance is left after five half-lives?
Two electrons are ejected in opposite directions from radioactive atoms in a sample of radioactive material. Let c denote the speed of light. Each electron has a speed of 0.67 c as measured by an observer in the laboratory. Their relative velocity is given by ______.
The half-life of a radioactive nuclide is 20 hrs. The fraction of the original activity that will remain after 40 hrs is ______.
If 10% of a radioactive material decay in 5 days, then the amount of original material left after 20 days is approximately :
Draw a graph showing the variation of decay rate with number of active nuclei.
Which sample, A or B shown in figure has shorter mean-life?
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
A piece of wood from the ruins of an ancient building was found to have a 14C activity of 12 disintegrations per minute per gram of its carbon content. The 14C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of 14C is 5760 years.
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is :
\[\ce{^38Sulphur ->[half-life][= 2.48h] ^{38}Cl ->[half-life][= 0.62h] ^38Air (stable)}\]
Assume that we start with 1000 38S nuclei at time t = 0. The number of 38Cl is of count zero at t = 0 and will again be zero at t = ∞ . At what value of t, would the number of counts be a maximum?
The activity R of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:
| t (h) | 0 | 1 | 2 | 3 | 4 |
| R (MBq) | 100 | 35.36 | 12.51 | 4.42 | 1.56 |
- Plot the graph of R versus t and calculate the half-life from the graph.
- Plot the graph of ln `(R/R_0)` versus t and obtain the value of half-life from the graph.
The radioactivity of an old sample of whisky due to tritium (half-life 12.5 years) was found to be only about 4% of that measured in a recently purchased bottle marked 10 years old. The age of a sample is ______ years.
The half-life of `""_82^210Pb` is 22.3 y. How long will it take for its activity 0 30% of the initial activity?
