Advertisements
Advertisements
प्रश्न
A radioactive isotope is being produced at a constant rate dN/dt = R in an experiment. The isotope has a half-life t1/2. Show that after a time t >> t1/2 the number of active nuclei will become constant. Find the value of this constant.
उत्तर
Given:
Half life period of isotope = t1/2
Disintegration constant, `lambda = 0.693/t_"1/2"`
Rate of Radio active decay (R) is given by
`R = "dN"/"dt"`
We are to show that after time t >> `t_"1/2"`the number of active nuclei is constant.
`("dN"/"dt")_"present" = R = ("dN"/"dt")_"decay"`
`therefore R = ("dN"/"dt")_"decay"`
Rate of radioactive decay, `R = lambdaN`
Here, λ = Radioactive decay constant
N = Constant number
`R = 0.693/t_"1/2" xx N`
⇒`Rt_"1/2" = 0.693 N`
⇒`N = (Rt_"1/2")/0.693`
This value of N should be constant.
APPEARS IN
संबंधित प्रश्न
(a) Write the basic nuclear process involved in the emission of β+ in a symbolic form, by a radioactive nucleus.
(b) In the reactions given below:
(i)`""_16^11C->_y^zB+x+v`
(ii)`""_6^12C+_6^12C->_a^20 Ne + _b^c He`
Find the values of x, y, and z and a, b and c.
A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value?
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive `""_6^14"C"` present with the stable carbon isotope `""_6^12"C"`. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of `""_6^14"C"` and the measured activity, the age of the specimen can be approximately estimated. This is the principle of `""_6^14"C"` dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
A source contains two phosphorous radio nuclides `""_15^32"P"` (T1/2 = 14.3d) and `""_15^33"P"` (T1/2 = 25.3d). Initially, 10% of the decays come from `""_15^33"P"`. How long one must wait until 90% do so?
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:
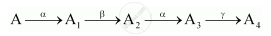
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A4?
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
The decay constant of a radioactive sample is λ. The half-life and the average-life of the sample are respectively
Calculate the maximum kinetic energy of the beta particle emitted in the following decay scheme:
12N → 12C* + e+ + v
12C* → 12C + γ (4.43MeV).
The atomic mass of 12N is 12.018613 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of `""_80^197`Hg (electron capture to `""_79^197`Au) is 1.8 × 10−4 S−1. (a) What is the half-life? (b) What is the average-life? (c) How much time will it take to convert 25% of this isotope of mercury into gold?
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Define one Becquerel.
A source contains two species of phosphorous nuclei, \[\ce{_15^32P}\] (T1/2 = 14.3 d) and \[\ce{_15^33P}\] (T1/2 = 25.3 d). At time t = 0, 90% of the decays are from \[\ce{_15^32P}\]. How much time has to elapse for only 15% of the decays to be from \[\ce{_15^32P}\]?
Which one of the following nuclei has shorter meant life?
After 1 hour, `(1/8)^"th"` of the initial mass of a certain radioactive isotope remains undecayed. The half-life of the isotopes is ______.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
Samples of two radioactive nuclides A and B are taken. λA and λB are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
- Initial rate of decay of A is twice the initial rate of decay of B and λA = λB.
- Initial rate of decay of A is twice the initial rate of decay of B and λA > λB.
- Initial rate of decay of B is twice the initial rate of decay of A and λA > λB.
- Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λB < λA.
What is the half-life period of a radioactive material if its activity drops to 1/16th of its initial value of 30 years?
