Advertisements
Advertisements
प्रश्न
In a radioactive decay, neither the atomic number nor the mass number changes. Which of the following particles is emitted in the decay?
विकल्प
Proton
Neutron
Electron
Photon
उत्तर
Photon
The atomic number and mass number of a nucleus is defined as the number of protons and the sum of the number of protons and neutrons present in the nucleus, respectively. Since in the decay, neither the atomic number nor the mass number change, it cannot be a beta-decay (release of electron, proton or neutron). Hence, the particle emitted can only be a photon.
APPEARS IN
संबंधित प्रश्न
Derive the mathematical expression for law of radioactive decay for a sample of a radioactive nucleus
Why is it found experimentally difficult to detect neutrinos in nuclear β-decay?
The half-life of `""_38^90 "Sr"` is 28 years. What is the disintegration rate of 15 mg of this isotope?
The radionuclide 11C decays according to
\[\ce{^11_6C -> ^11_5B + e+ + \text{v}}\] : T1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV.
Given the mass values: `"m"(""_6^11"C") = 11.011434 u and "m"(""_6^11"B") = 11.009305 "u"`
Calculate Q and compare it with the maximum energy of the positron emitted.
The Q value of a nuclear reaction A + b → C + d is defined by
Q = [mA+ mb − mC − md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
\[\ce{^12_6C + ^12_6C ->^20_10Ne + ^4_2He}\]
Atomic masses are given to be
`"m"(""_1^2"H")` = 2.014102 u
`"m"(""_1^3"H")` = 3.016049 u
`"m"(""_6^12C)` = 12.000000 u
`"m"(""_10^20"Ne")` = 19.992439 u
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:
\[\ce{^223_88Ra -> ^209_82Pb + ^14_6C}\]
\[\ce{^223_88 Ra -> ^219_86 Rn + ^4_2He}\]
Calculate the Q-values for these decays and determine that both are energetically allowed.
Two different radioactive elements with half lives T1 and T2 have N1 and N2 undecayed atoms respectively present at a given instant. Derive an expression for the ratio of their activities at this instant in terms of N1 and N2 ?
28Th emits an alpha particle to reduce to 224Ra. Calculate the kinetic energy of the alpha particle emitted in the following decay:
`""^228"Th" → ""^224"Ra"^(∗) + alpha`
`""^224"Ra"^(∗) → ""^224"Ra" + γ (217 "keV")`.
Atomic mass of 228Th is 228.028726 u, that of 224Ra is 224.020196 u and that of `""_2^4H` is 4.00260 u.
(Use Mass of proton mp = 1.007276 u, Mass of `""_1^1"H"` atom = 1.007825 u, Mass of neutron mn = 1.008665 u, Mass of electron = 0.0005486 u ≈ 511 keV/c2,1 u = 931 MeV/c2.)
The decay constant of 238U is 4.9 × 10−18 S−1. (a) What is the average-life of 238U? (b) What is the half-life of 238U? (c) By what factor does the activity of a 238U sample decrease in 9 × 109 years?
57Co decays to 57Fe by β+- emission. The resulting 57Fe is in its excited state and comes to the ground state by emitting γ-rays. The half-life of β+- decay is 270 days and that of the γ-emissions is 10−8 s. A sample of 57Co gives 5.0 × 109 gamma rays per second. How much time will elapse before the emission rate of gamma rays drops to 2.5 × 109per second?
Consider the situation of the previous problem. Suppose the production of the radioactive isotope starts at t = 0. Find the number of active nuclei at time t.
Obtain a relation between the half-life of a radioactive substance and decay constant (λ).
Disintegration rate of a sample is 1010 per hour at 20 hours from the start. It reduces to 6.3 x 109 per hour after 30 hours. Calculate its half-life and the initial number of radioactive atoms in the sample.
Obtain an expression for the decay law of radioactivity. Hence show that the activity A(t) =λNO e-λt.
Two radioactive materials Y1 and Y2 have decay constants '5`lambda`' and `lambda` respectively. Initially they have same number of nuclei. After time 't', the ratio of number of nuclei of Y1 to that of Y2 is `1/"e"`, then 't' is equal to ______.
Draw a graph showing the variation of decay rate with number of active nuclei.
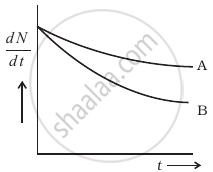
Which sample, A or B shown in figure has shorter mean-life?
The radioactivity of an old sample of whisky due to tritium (half-life 12.5 years) was found to be only about 4% of that measured in a recently purchased bottle marked 10 years old. The age of a sample is ______ years.
