Advertisements
Advertisements
प्रश्न
The count rate of nuclear radiation coming from a radiation coming from a radioactive sample containing 128I varies with time as follows.
| Time t (minute): | 0 | 25 | 50 | 75 | 100 |
| Ctount rate R (109 s−1): | 30 | 16 | 8.0 | 3.8 | 2.0 |
(a) Plot In (R0/R) against t. (b) From the slope of the best straight line through the points, find the decay constant λ. (c) Calculate the half-life t1/2.
उत्तर
(a) For t = 0,
`"In" (R_0/R) = "In" ((30 xx 10^9)/(30 xx 10^9)) = 0`
For t = 25 s,
`"In" (R_0/R_2) = "In" ((30 xx 10^9)/(16 xx 10^9)) = 0.63`
For t = 50 s,
`"In" (R_0/R_3) = "In" ((30 xx 10^9)/(8 xx 10^9)) = 1.35`
For t = 75 s,
`"In" (R_0/R_4) = "In" ((30 xx 10^9)/(3.8 xx 10^9)) = 2.06`
For t = 100 s,
`"In" (R_0/R_5) = "In" ((30 xx 10^9)/(2 xx 10^9)) = 2.7`
The required graph is shown below.
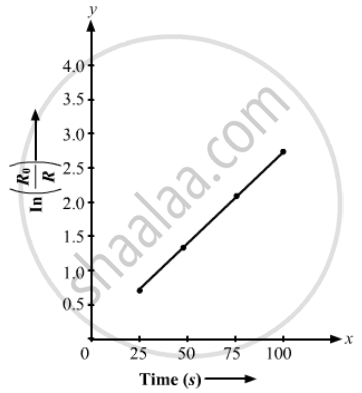
(b) Slope of the graph = 0.028
∴ Decay constant, `lambda` = 0.028 `"min"^-1`
The half-life period (`T_"1/2"`) is given by
`T_"1/2" = 0.693/lambda`
= `0.693/0.028 = 25 "min"`
APPEARS IN
संबंधित प्रश्न
Write nuclear reaction equation for α-decay of `""_88^226"Ra"`.
Write nuclear reaction equation for β−-decay of `""_83^210"Bi"`.
Write nuclear reaction equation for β+-decay of `""_6^11"C"`.
Write nuclear reaction equation for β+-decay of `""_43^97"Tc"`.
Write nuclear reaction equation for electron capture of `""_54^120"Xe"`.
A radioactive nucleus has a decay constant λ = 0.3465 (day)–1. How long would it take the nucleus to decay to 75% of its initial amount?
Define ‘activity’ of a radioactive material and write its S.I. units.
The half-life of 199Au is 2.7 days. (a) Find the activity of a sample containing 1.00 µg of 198Au. (b) What will be the activity after 7 days? Take the atomic weight of 198Au to be 198 g mol−1.
Radioactive 131I has a half-life of 8.0 days. A sample containing 131I has activity 20 µCi at t = 0. (a) What is its activity at t = 4 days? (b) What is its decay constant at t = 4.0 days?
A certain sample of a radioactive material decays at the rate of 500 per second at a certain time. The count rate falls to 200 per second after 50 minutes. (a) What is the decay constant of the sample? (b) What is its half-life?
`""_80^197`Hg decay to `""_79^197`Au through electron capture with a decay constant of 0.257 per day. (a) What other particle or particles are emitted in the decay? (b) Assume that the electron is captured from the K shell. Use Moseley's law √v = a(Z − b) with a = 4.95 × 107s−1/2 and b = 1 to find the wavelength of the Kα X-ray emitted following the electron capture.
`""_83^212"Bi"` can disintegrate either by emitting an α-particle of by emitting a β−-particle. (a) Write the two equations showing the products of the decays. (b) The probabilities of disintegration α-and β-decays are in the ratio 7/13. The overall half-life of 212Bi is one hour. If 1 g of pure 212Bi is taken at 12.00 noon, what will be the composition of this sample at 1 P.m. the same day?
A sample contains a mixture of 108Ag and 110Ag isotopes each having an activity of 8.0 × 108 disintegration per second. 110Ag is known to have larger half-life than 108Ag. The activity A is measured as a function of time and the following data are obtained.
| Time (s) |
Activity (A) (108 disinte- grations s−1) |
Time (s) |
Activity (A 108 disinte-grations s−1) |
| 20 40 60 80 100 |
11.799 9.1680 7.4492 6.2684 5.4115 |
200 300 400 500 |
3.0828 1.8899 1.1671 0.7212 |
(a) Plot ln (A/A0) versus time. (b) See that for large values of time, the plot is nearly linear. Deduce the half-life of 110Ag from this portion of the plot. (c) Use the half-life of 110Ag to calculate the activity corresponding to 108Ag in the first 50 s. (d) Plot In (A/A0) versus time for 108Ag for the first 50 s. (e) Find the half-life of 108Ag.
In a gamma ray emission from nucleus :
Copy and complete the following table for a radioactive element whose half-life is 10 minutes. Assume that you have 30g of this element at t = 0.

A radioactive substance decays to 1/16th of its initial mass in 40 days. The half-life of the substance, in days, is:
The half-life of a certain radioactive element is 3.465 days. Find its disintegration constant.
Half life of a certain radioactive material is 8 hours.
If one starts with 600 g of this substance, how much of it will disintegrate in one day?
