Advertisements
Advertisements
प्रश्न
Natural water contains a small amount of tritium (`""_1^3H`). This isotope beta-decays with a half-life of 12.5 years. A mountaineer while climbing towards a difficult peak finds debris of some earlier unsuccessful attempt. Among other things he finds a sealed bottled of whisky. On returning, he analyses the whisky and finds that it contains only 1.5 per cent of the `""_1^3H` radioactivity as compared to a recently purchased bottle marked '8 years old'. Estimate the time of that unsuccessful attempt.
उत्तर
Given:
Half-life time of tritium, `T_"1/2"` = 12.5 years
Disintegration constant, `lambda = 0.693/12.5` per year
Let A0 be the activity, when the bottle was manufactured.
Activity after 8 years (A) is given by
`A = A_0e^((-0.693)/(12.5) xx 8)` .....(1)
Let us consider that the mountaineering had taken place t years ago.
Then, activity of the bottle (A') on the mountain is given by
`A' = A_0e^(-lambdat)`
Here, A' = (Activity of the bottle manufactured 8 years ago) × 1.5 %
`A' = A_0e^((-0.693)/(12.5) xx 8) xx 0.015` ...(2)
Comparing (1) and (2)
`(-0.693)/12.5 t = (-0.6931 xx 8)/12.5 + "In" [0.015]`
⇒ `(-0.693)/12.5 t = (-0.693)/12.5 xx 8 - 4.1997`
⇒ `0.639 t = 58.040`
⇒ t = 83.75 years
APPEARS IN
संबंधित प्रश्न
For the past some time, Aarti had been observing some erratic body movement, unsteadiness and lack of coordination in the activities of her sister Radha, who also used to complain of severe headache occasionally. Aarti suggested to her parents to get a medical check-up of Radha. The doctor thoroughly examined Radha and diagnosed that she has a brain tumour.
(a) What, according to you, are the values displayed by Aarti?
(b) How can radioisotopes help a doctor to diagnose brain tumour?
Write nuclear reaction equation for α-decay of `""_88^226"Ra"`.
Write nuclear reaction equation for α-decay of `""_94^242"Pu"`.
Write nuclear reaction equation for β−-decay of `""_83^210"Bi"`.
A radioactive nucleus has a decay constant λ = 0.3465 (day)–1. How long would it take the nucleus to decay to 75% of its initial amount?
Define ‘activity’ of a radioactive material and write its S.I. units.
The sequence of stepwise decay of a radioactive nucleus is
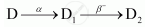
If the atomic number and mass number of D2 are 71 and 176 respectively, what are their corresponding values of D?
State the law of radioactive decay. hence derive the relation N = Noe-λt . Represent it graphically.
A certain sample of a radioactive material decays at the rate of 500 per second at a certain time. The count rate falls to 200 per second after 50 minutes. (a) What is the decay constant of the sample? (b) What is its half-life?
`""_80^197`Hg decay to `""_79^197`Au through electron capture with a decay constant of 0.257 per day. (a) What other particle or particles are emitted in the decay? (b) Assume that the electron is captured from the K shell. Use Moseley's law √v = a(Z − b) with a = 4.95 × 107s−1/2 and b = 1 to find the wavelength of the Kα X-ray emitted following the electron capture.
The count rate of nuclear radiation coming from a radiation coming from a radioactive sample containing 128I varies with time as follows.
| Time t (minute): | 0 | 25 | 50 | 75 | 100 |
| Ctount rate R (109 s−1): | 30 | 16 | 8.0 | 3.8 | 2.0 |
(a) Plot In (R0/R) against t. (b) From the slope of the best straight line through the points, find the decay constant λ. (c) Calculate the half-life t1/2.
238U decays to 206Pb with a half-life of 4.47 × 109 y. This happens in a number of steps. Can you justify a single half for this chain of processes? A sample of rock is found to contain 2.00 mg of 238U and 0.600 mg of 206Pb. Assuming that all the lead has come from uranium, find the life of the rock.
A charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ. Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
In a gamma ray emission from nucleus :
The half-life of radium is 1550 years. Calculate its disintegration constant (`lambda`) .
Copy and complete the following table for a radioactive element whose half-life is 10 minutes. Assume that you have 30g of this element at t = 0.

The half-life of a certain radioactive element is 3.465 days. Find its disintegration constant.
Half life of a certain radioactive material is 8 hours.
If one starts with 600 g of this substance, how much of it will disintegrate in one day?
