Advertisements
Advertisements
प्रश्न
The count rate of nuclear radiation coming from a radiation coming from a radioactive sample containing 128I varies with time as follows.
| Time t (minute): | 0 | 25 | 50 | 75 | 100 |
| Ctount rate R (109 s−1): | 30 | 16 | 8.0 | 3.8 | 2.0 |
(a) Plot In (R0/R) against t. (b) From the slope of the best straight line through the points, find the decay constant λ. (c) Calculate the half-life t1/2.
उत्तर
(a) For t = 0,
`"In" (R_0/R) = "In" ((30 xx 10^9)/(30 xx 10^9)) = 0`
For t = 25 s,
`"In" (R_0/R_2) = "In" ((30 xx 10^9)/(16 xx 10^9)) = 0.63`
For t = 50 s,
`"In" (R_0/R_3) = "In" ((30 xx 10^9)/(8 xx 10^9)) = 1.35`
For t = 75 s,
`"In" (R_0/R_4) = "In" ((30 xx 10^9)/(3.8 xx 10^9)) = 2.06`
For t = 100 s,
`"In" (R_0/R_5) = "In" ((30 xx 10^9)/(2 xx 10^9)) = 2.7`
The required graph is shown below.
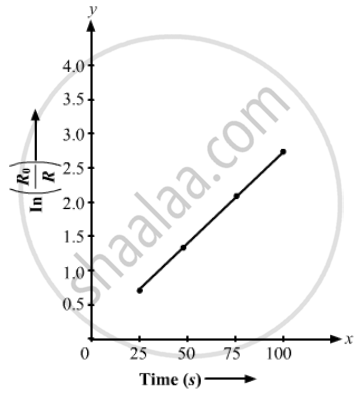
(b) Slope of the graph = 0.028
∴ Decay constant, `lambda` = 0.028 `"min"^-1`
The half-life period (`T_"1/2"`) is given by
`T_"1/2" = 0.693/lambda`
= `0.693/0.028 = 25 "min"`
APPEARS IN
संबंधित प्रश्न
For the past some time, Aarti had been observing some erratic body movement, unsteadiness and lack of coordination in the activities of her sister Radha, who also used to complain of severe headache occasionally. Aarti suggested to her parents to get a medical check-up of Radha. The doctor thoroughly examined Radha and diagnosed that she has a brain tumour.
(a) What, according to you, are the values displayed by Aarti?
(b) How can radioisotopes help a doctor to diagnose brain tumour?
Write nuclear reaction equation for α-decay of `""_88^226"Ra"`.
Write nuclear reaction equation for β+-decay of `""_43^97"Tc"`.
A radioactive nucleus has a decay constant λ = 0.3465 (day)–1. How long would it take the nucleus to decay to 75% of its initial amount?
Define ‘activity’ of a radioactive material and write its S.I. units.
The sequence of stepwise decay of a radioactive nucleus is
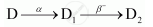
If the atomic number and mass number of D2 are 71 and 176 respectively, what are their corresponding values of D?
Radioactive 131I has a half-life of 8.0 days. A sample containing 131I has activity 20 µCi at t = 0. (a) What is its activity at t = 4 days? (b) What is its decay constant at t = 4.0 days?
The half-life of a radioisotope is 10 h. Find the total number of disintegration in the tenth hour measured from a time when the activity was 1 Ci.
The selling rate of a radioactive isotope is decided by its activity. What will be the second-hand rate of a one month old 32P(t1/2 = 14.3 days) source if it was originally purchased for 800 rupees?
A vessel of volume 125 cm3 contains tritium (3H, t1/2 = 12.3 y) at 500 kPa and 300 K. Calculate the activity of the gas.
4 × 1023 tritium atoms are contained in a vessel. The half-life of decay tritium nuclei is 12.3 y. Find (a) the activity of the sample, (b) the number of decay in the next 10 hours (c) the number of decays in the next 6.15 y.
238U decays to 206Pb with a half-life of 4.47 × 109 y. This happens in a number of steps. Can you justify a single half for this chain of processes? A sample of rock is found to contain 2.00 mg of 238U and 0.600 mg of 206Pb. Assuming that all the lead has come from uranium, find the life of the rock.
A charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ. Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
Radioactive isotopes are produced in a nuclear physics experiment at a constant rate dN/dt = R. An inductor of inductance 100 mH, a resistor of resistance 100 Ω and a battery are connected to form a series circuit. The circuit is switched on at the instant the production of radioactive isotope starts. It is found that i/N remains constant in time where i is the current in the circuit at time t and N is the number of active nuclei at time t. Find the half-life of the isotope.
`""_83^212"Bi"` can disintegrate either by emitting an α-particle of by emitting a β−-particle. (a) Write the two equations showing the products of the decays. (b) The probabilities of disintegration α-and β-decays are in the ratio 7/13. The overall half-life of 212Bi is one hour. If 1 g of pure 212Bi is taken at 12.00 noon, what will be the composition of this sample at 1 P.m. the same day?
A sample contains a mixture of 108Ag and 110Ag isotopes each having an activity of 8.0 × 108 disintegration per second. 110Ag is known to have larger half-life than 108Ag. The activity A is measured as a function of time and the following data are obtained.
| Time (s) |
Activity (A) (108 disinte- grations s−1) |
Time (s) |
Activity (A 108 disinte-grations s−1) |
| 20 40 60 80 100 |
11.799 9.1680 7.4492 6.2684 5.4115 |
200 300 400 500 |
3.0828 1.8899 1.1671 0.7212 |
(a) Plot ln (A/A0) versus time. (b) See that for large values of time, the plot is nearly linear. Deduce the half-life of 110Ag from this portion of the plot. (c) Use the half-life of 110Ag to calculate the activity corresponding to 108Ag in the first 50 s. (d) Plot In (A/A0) versus time for 108Ag for the first 50 s. (e) Find the half-life of 108Ag.
In a gamma ray emission from nucleus :
Plot a graph showing the variation of undecayed nuclei N versus time t. From the graph, find out how one can determine the half-life and average life of the radioactive nuclei.
Half life of a certain radioactive material is 8 hours.
If one starts with 600 g of this substance, how much of it will disintegrate in one day?
