Advertisements
Advertisements
प्रश्न
Plot a graph showing the variation of undecayed nuclei N versus time t. From the graph, find out how one can determine the half-life and average life of the radioactive nuclei.
उत्तर १
N = N0e-λt
for half life `N = (N_0) /2 " and " t = t_(1/2)`
`N_o/2 = N_o e^(-lambda t_(1/2))`
`2 = e^(lambda t_(1/2))` (Inverting)
`log_e 2 = lambda t_(1/2)`
0.693` = lambda t_(1/2)`
`t_(1/2) = lambda/0.693`
उत्तर २
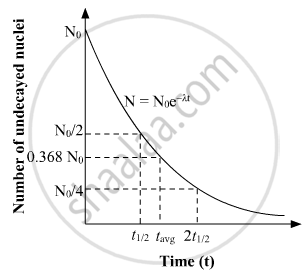
The half-life of a radioactive sample is the amount of time required for it to get decayed to 50% of its original amount and the average life is the amount of time required for it to get decayed to 36.8% of its original amount. If No is the original amount of the radioactive material then the value of time on the x-axis at which N=No/2 on the y-axis, will be the value of half-life and the value of time on the x-axis for which N = 0.368 No will give the value of average life for the radioactive element.
Hence by taking the values on the x-axis for N=No/2 & N = 0.368 No, we can simply find the value of half-life and average life from the given graph.
संबंधित प्रश्न
Write nuclear reaction equation for β+-decay of `""_43^97"Tc"`.
Draw graphs showing variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
A radioactive nucleus has a decay constant λ = 0.3465 (day)–1. How long would it take the nucleus to decay to 75% of its initial amount?
State the law of radioactive decay. hence derive the relation N = Noe-λt . Represent it graphically.
Radioactive 131I has a half-life of 8.0 days. A sample containing 131I has activity 20 µCi at t = 0. (a) What is its activity at t = 4 days? (b) What is its decay constant at t = 4.0 days?
A certain sample of a radioactive material decays at the rate of 500 per second at a certain time. The count rate falls to 200 per second after 50 minutes. (a) What is the decay constant of the sample? (b) What is its half-life?
`""_80^197`Hg decay to `""_79^197`Au through electron capture with a decay constant of 0.257 per day. (a) What other particle or particles are emitted in the decay? (b) Assume that the electron is captured from the K shell. Use Moseley's law √v = a(Z − b) with a = 4.95 × 107s−1/2 and b = 1 to find the wavelength of the Kα X-ray emitted following the electron capture.
The count rate of nuclear radiation coming from a radiation coming from a radioactive sample containing 128I varies with time as follows.
| Time t (minute): | 0 | 25 | 50 | 75 | 100 |
| Ctount rate R (109 s−1): | 30 | 16 | 8.0 | 3.8 | 2.0 |
(a) Plot In (R0/R) against t. (b) From the slope of the best straight line through the points, find the decay constant λ. (c) Calculate the half-life t1/2.
A charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ. Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
Half-life of a certain radioactive material is 8 hours.
Find the disintegration constant of this material.
