Advertisements
Advertisements
प्रश्न
Plot a graph showing the variation of undecayed nuclei N versus time t. From the graph, find out how one can determine the half-life and average life of the radioactive nuclei.
उत्तर १
N = N0e-λt
for half life `N = (N_0) /2 " and " t = t_(1/2)`
`N_o/2 = N_o e^(-lambda t_(1/2))`
`2 = e^(lambda t_(1/2))` (Inverting)
`log_e 2 = lambda t_(1/2)`
0.693` = lambda t_(1/2)`
`t_(1/2) = lambda/0.693`
उत्तर २
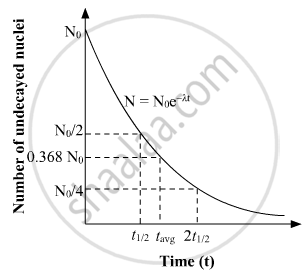
The half-life of a radioactive sample is the amount of time required for it to get decayed to 50% of its original amount and the average life is the amount of time required for it to get decayed to 36.8% of its original amount. If No is the original amount of the radioactive material then the value of time on the x-axis at which N=No/2 on the y-axis, will be the value of half-life and the value of time on the x-axis for which N = 0.368 No will give the value of average life for the radioactive element.
Hence by taking the values on the x-axis for N=No/2 & N = 0.368 No, we can simply find the value of half-life and average life from the given graph.
संबंधित प्रश्न
Write nuclear reaction equation for β−-decay of `""_15^32"P"`.
Write nuclear reaction equation for β+-decay of `""_6^11"C"`.
Plot a graph showing variation of activity of a given radioactive sample with time.
Radioactive 131I has a half-life of 8.0 days. A sample containing 131I has activity 20 µCi at t = 0. (a) What is its activity at t = 4 days? (b) What is its decay constant at t = 4.0 days?
The half-life of a radioisotope is 10 h. Find the total number of disintegration in the tenth hour measured from a time when the activity was 1 Ci.
In an agricultural experiment, a solution containing 1 mole of a radioactive material (t1/2= 14.3 days) was injected into the roots of a plant. The plant was allowed 70 hours to settle down and then activity was measured in its fruit. If the activity measured was 1 µCi, what per cent of activity is transmitted from the root to the fruit in steady state?
The count rate of nuclear radiation coming from a radiation coming from a radioactive sample containing 128I varies with time as follows.
| Time t (minute): | 0 | 25 | 50 | 75 | 100 |
| Ctount rate R (109 s−1): | 30 | 16 | 8.0 | 3.8 | 2.0 |
(a) Plot In (R0/R) against t. (b) From the slope of the best straight line through the points, find the decay constant λ. (c) Calculate the half-life t1/2.
4 × 1023 tritium atoms are contained in a vessel. The half-life of decay tritium nuclei is 12.3 y. Find (a) the activity of the sample, (b) the number of decay in the next 10 hours (c) the number of decays in the next 6.15 y.
Radioactive isotopes are produced in a nuclear physics experiment at a constant rate dN/dt = R. An inductor of inductance 100 mH, a resistor of resistance 100 Ω and a battery are connected to form a series circuit. The circuit is switched on at the instant the production of radioactive isotope starts. It is found that i/N remains constant in time where i is the current in the circuit at time t and N is the number of active nuclei at time t. Find the half-life of the isotope.
The half-life of radium is 1550 years. Calculate its disintegration constant (`lambda`) .
