Advertisements
Advertisements
प्रश्न
The half-life of a radioisotope is 10 h. Find the total number of disintegration in the tenth hour measured from a time when the activity was 1 Ci.
उत्तर
Given:
Half-life of radioisotope,`T_(1"/"2)` = 10 hrs
Initial activity, `A_0` = 1 Ci
Disintegration constant, `lambda = 0.693/(10 xx 3600) "s"^-1`
Activity of radioactive sample,
`A = A_0e^(-lambdat)`
Here, A0 = Initial activity
`lambda` = Disintegration constant
t = Time taken
After 9 hours,
Activity , `A = A_0e^(-lambdat) = 1 xx e^(-0.693/(10 xx 3600) xx 9 = 0.536` Ci
`therefore` Number of Atoms left , N = `A/lambda = (0.536 xx 10 xx 3.7 xx 10^10 xx 3600)/0.693 = 103.023 xx 10^13` After 10 hrs
Activity , A " `= A_0e^(-lambdat)`
= `1 xx e^(-0.693/10 xx 10) = 0.5` Ci
Number of atoms left after the 10th hour (`N` ")will be
A" = `lambdaN` "
N" = A"/`lambda`
= `(0.5 xx 3.7 xx 10^10 xx 3.600)/(0.693"/"10)`
= `26.37 xx 10^10 xx 3600 = 96.103 xx 10^13`
Number of disintegrations = (103.023 − 96.103) × 1013
= 6.92 × 1013
APPEARS IN
संबंधित प्रश्न
For the past some time, Aarti had been observing some erratic body movement, unsteadiness and lack of coordination in the activities of her sister Radha, who also used to complain of severe headache occasionally. Aarti suggested to her parents to get a medical check-up of Radha. The doctor thoroughly examined Radha and diagnosed that she has a brain tumour.
(a) What, according to you, are the values displayed by Aarti?
(b) How can radioisotopes help a doctor to diagnose brain tumour?
Write nuclear reaction equation for α-decay of `""_94^242"Pu"`.
Write nuclear reaction equation for electron capture of `""_54^120"Xe"`.
Plot a graph showing variation of activity of a given radioactive sample with time.
The sequence of stepwise decay of a radioactive nucleus is
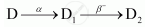
If the atomic number and mass number of D2 are 71 and 176 respectively, what are their corresponding values of D?
State the law of radioactive decay. hence derive the relation N = Noe-λt . Represent it graphically.
The half-life of 199Au is 2.7 days. (a) Find the activity of a sample containing 1.00 µg of 198Au. (b) What will be the activity after 7 days? Take the atomic weight of 198Au to be 198 g mol−1.
Radioactive 131I has a half-life of 8.0 days. A sample containing 131I has activity 20 µCi at t = 0. (a) What is its activity at t = 4 days? (b) What is its decay constant at t = 4.0 days?
`""_80^197`Hg decay to `""_79^197`Au through electron capture with a decay constant of 0.257 per day. (a) What other particle or particles are emitted in the decay? (b) Assume that the electron is captured from the K shell. Use Moseley's law √v = a(Z − b) with a = 4.95 × 107s−1/2 and b = 1 to find the wavelength of the Kα X-ray emitted following the electron capture.
In an agricultural experiment, a solution containing 1 mole of a radioactive material (t1/2= 14.3 days) was injected into the roots of a plant. The plant was allowed 70 hours to settle down and then activity was measured in its fruit. If the activity measured was 1 µCi, what per cent of activity is transmitted from the root to the fruit in steady state?
Natural water contains a small amount of tritium (`""_1^3H`). This isotope beta-decays with a half-life of 12.5 years. A mountaineer while climbing towards a difficult peak finds debris of some earlier unsuccessful attempt. Among other things he finds a sealed bottled of whisky. On returning, he analyses the whisky and finds that it contains only 1.5 per cent of the `""_1^3H` radioactivity as compared to a recently purchased bottle marked '8 years old'. Estimate the time of that unsuccessful attempt.
A charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ. Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
Radioactive isotopes are produced in a nuclear physics experiment at a constant rate dN/dt = R. An inductor of inductance 100 mH, a resistor of resistance 100 Ω and a battery are connected to form a series circuit. The circuit is switched on at the instant the production of radioactive isotope starts. It is found that i/N remains constant in time where i is the current in the circuit at time t and N is the number of active nuclei at time t. Find the half-life of the isotope.
The half-life of radium is 1550 years. Calculate its disintegration constant (`lambda`) .
Copy and complete the following table for a radioactive element whose half-life is 10 minutes. Assume that you have 30g of this element at t = 0.

Plot a graph showing the variation of undecayed nuclei N versus time t. From the graph, find out how one can determine the half-life and average life of the radioactive nuclei.
A radioactive substance decays to 1/16th of its initial mass in 40 days. The half-life of the substance, in days, is:
A nucleus with Z = 92 emits the following in a sequence:
α, β‾, β‾, α, α, α, α, α, β‾, β‾, α, β+, β+, α
Then Z of the resulting nucleus is ______.
