Advertisements
Advertisements
प्रश्न
- Consider circuit in figure. How much energy is absorbed by electrons from the initial state of no current (ignore thermal motion) to the state of drift velocity?
- Electrons give up energy at the rate of RI2 per second to the thermal energy. What time scale would one associate with energy in problem (a)? n = no of electron/volume = 1029/m3, length of circuit = 10 cm, cross-section = A = (1mm)2
Advertisements
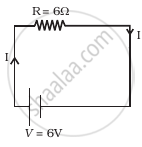
उत्तर
a. Relation between current and drift velocity is given by I = ne Avd, where vd is the drift speed of electrons and n is the number density of electrons.
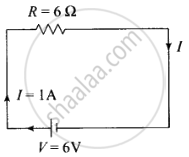
According to the Ohm's law current in the circuit
I = V/R
I = 6 V/6 Ω = 1 A
But, I = ne Avd
or vd = `I/("ne A")`
On substituting the values,
For, n = number of electrons/volume = 1029/m3
Length of circuit = 10 cm, cross-section = A = (1 mm)2
`v_d = 1/(10^29 xx 16 xx 10^-19 xx 10^-6)`
= `1/1.6 xx 10^-4` m/s
Therefore, the energy absorbed in the form of KE is given by
Total KE = KE of 1 electron × no. of electrons
KE = `1/2 m_e v_d^2 xx n Al`
= `1/2 xx 9.1 xx 10^31 xx 1/2.56 xx 10^-8 xx 10^29 xx 10^-6 xx 10^-1`
= `2 xx 10^-17 J`
b. Ohmic loss (power loss) is `P = I^2R = 6 xx 1^2 = 6 W = 6 J/s`
Since, the energy dissipated per unit time is the power dissipated.
So, `P = E/t`
Therefore, `E = P xx t`
or `t = E/P = (2 xx 10^17)/6 = 10^17 s`
Important point: The energy dissipated per unit time is the power dissipated `P = (ΔW)/(Δt)`
The power across a resistor is P = I2R.
APPEARS IN
संबंधित प्रश्न
Define the term drift velocity.
Write its (‘mobility’ of charge carriers) S.I. unit
On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
A conductor of length ‘l’ is connected to a dc source of potential ‘V’. If the length of the conductor is tripled by gradually stretching it, keeping ‘V’ constant, how will (i) drift speed of electrons and (ii) resistance of the conductor be affected? Justify your answer.
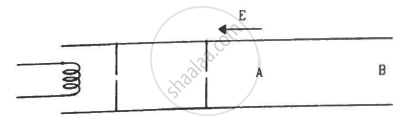
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure. The two stops at the left ensure that the electron beam has a uniform cross-section.
A current of 1.0 A exists in a copper wire of cross-section 1.0 mm2. Assuming one free electron per atom, calculate the drift speed of the free electrons in the wire. The density of copper is 9000 kg m–3.
Consider a wire of length 4 m and cross-sectional area 1 mm2 carrying a current of 2 A. If each cubic metre of the material contains 1029 free electrons, find the average time taken by an electron to cross the length of the wire.
Obtain the expression for the current flowing through a conductor having number density of the electron n, area of cross-section A in terms of the drift velocity vd .
Metals are good conductor of heat than insulator because
Amount of charge in coulomb required to deposit one gram equivalent of substance by electrolysis is:-
The identical conductors maintained at same temperature are given potential difference in the ratio 1 : 2. Then the ratio of their drift velocities is ______.
The relaxation time τ is nearly independent of applied E field whereas it changes significantly with temperature T. First fact is (in part) responsible for Ohm’s law whereas the second fact leads to variation of ρ with temperature. Elaborate why?
Derive an expression for resistivity of a conductor in terms of the number density of charge carriers in the conductor and relaxation time.
Explain how free electrons in a metal at constant temperature attain an average velocity under the action of an electric field. Hence, obtain an expression for it.
A potential difference (V) is applied across a conductor of length 'L' and cross-sectional area 'A'.
How will the drift velocity of electrons and the current density be affected if another identical conductor of the same material were connected in series with the first conductor? Justify your answers.
Two conductors, made of the same material have equal lengths but different cross-sectional areas A1 and A2 (A1 > A2). They are connected in parallel across a cell. Show that the drift velocities of electrons in two conductors are equal.
