Advertisements
Advertisements
प्रश्न
On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
उत्तर
Free electrons are in continuous random motion. They undergo change in direction at each collision and the thermal velocities are randomly distributed in all directions.
∴ Average thermal velocity
`u=(u_1+u_2...u_n)/n = 0 `

The electric field E exerts an electrostatic force ‘−Ee’
The acceleration of each electron is
`veca=(-evecE)/m `
Here,
m → Mass of an electron
e → Charge on an electron
Drift velocity is given by
`vecv_d=(v_1+v_2+....+v_n)/n`
`vec(V_d)=((vecu_1+vecat_1)+(vecu_2+vecat_2)+...+(vecu_n_vecat_n))/n`
Here,
`vecu_1,vecu_2->` Thermal velocities of the electrons
`vecatau_1,vectau_2` Velocities acquired by electrons
τ1, τ2 → Time elapsed after the collision
`vecv_d=(vecu_1+vecu_2+...vecu_n)/n+(veca(t_1+t_2+...t_n))/n`
Since`(vecu_1+vecu_2+...+u_n)/n=0`
∴ vd = a τ .....(3)
Here `t=(t_1+t_2+t_3...+t_n)/n` is the average time elapsed.
Substituting for a from equation (2),
`vec(V_d)=(-evecE)/mt...(4)`
Because of the external electric field, electrons are accelerated. They move from one place to another and current is produced.
For small intervals dt, we have
Idt = −q
Here, q is the total c
(i) The average velocity of all the free electrons in the conductor with which they get drifted towards the positive end of the conductor under the influence of an external electric field is called the drift velocity.
(ii) Free electrons are in continuous random motion. They undergo a change in direction at each collision and the thermal velocities are randomly distributed in all directions.
∴ Average thermal velocity
`u=(u_1+u_2...u_n)/n = 0 `

The electric field E exerts an electrostatic force ‘−Ee’
The acceleration of each electron is
`veca=(-evecE)/m `
Here,
m → Mass of an electron
e → Charge on an electron
Drift velocity is given by
`vecv_d=(v_1+v_2+....+v_n)/n`
`vec(V_d)=((vecu_1+vecat_1)+(vecu_2+vecat_2)+...+(vecu_n_vecat_n))/n`
Here,
`vecu_1,vecu_2->` Thermal velocities of the electrons
`vecatau_1,vecatau_2->` Velocities acquired by electrons
τ1, τ2 → Time elapsed after the collision
`vecv_d=(vecu_1+vecu_2+...vecu_n)/n+(veca(t_1+t_2+...t_n))/n`
Since`(vecu_1+vecu_2+...+u_n)/n=0`
∴ vd = a τ .....(3)
Here `t=(t_1+t_2+t_3...+t_n)/n`is the average time elapsed.
Substituting for a from equation (2),
`vec(V_d)=(-evecE)/mt...(4)`
Because of the external electric field, electrons are accelerated. They move from one place to another and current is produced.
For small intervals dt, we have
Idt = −q
Here, q is the total charge flowing.
Let n be the free electrons per unit area. Then, the total charge crossing area A in time dt is given by
Idt = neAvddt
Substituting the value of vd, we obtain
`Idt= n eA(-eE/m) dt`
I/A = J
Here, J is the current density.
`|J|=n e^2/m |E|T`
From Ohm’s law,
J = σE
Here, σ is the conductivity of the material through which the current is flowing.
Thus,
`sigma =(n e^2)/mT`
`sigma=1/rho`
or
`rho=1/sigma`
Substituting the value of conductivity, we obtain
`rho=m/(n e^2T)`
Here, τ is the relaxation time.
संबंधित प्रश्न
Derive an expression for drift velocity of free electrons.
How does drift velocity of electrons in a metallic conductor vary with increase in temperature? Explain.
When electrons drift in a metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction?
A conductor of length ‘l’ is connected to a dc source of potential ‘V’. If the length of the conductor is tripled by gradually stretching it, keeping ‘V’ constant, how will (i) drift speed of electrons and (ii) resistance of the conductor be affected? Justify your answer.
Electrons are emitted by a hot filament and are accelerated by an electric field, as shown in the figure. The two stops at the left ensure that the electron beam has a uniform cross-section.
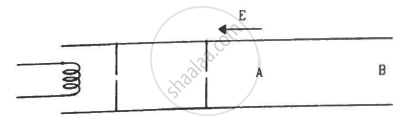
Consider the following statements.
(A) Free-electron density is different in different metals.
(B) Free-electron density in a metal depends on temperature.
Peltier Effect is caused _______________ .
Is the momentum conserved when charge crosses a junction in an electric circuit? Why or why not?
Derive an expression for resistivity of a conductor in terms of the number density of charge carriers in the conductor and relaxation time.
A potential difference (V) is applied across a conductor of length 'L' and cross-sectional area 'A'.
How will the drift velocity of electrons and the current density be affected if another identical conductor of the same material were connected in series with the first conductor? Justify your answers.
The drift velocity of electrons in a conductor connected to a battery is given by vd = `(−"eE" τ)/"m"`. Here, e is the charge of the electron, E is the electric field, τ is the average time between collisions and m is the mass of the electron.
Based on this, answer the following:
- How does the drift velocity change with a change in the potential difference across the conductor?
- A copper wire of length 'l' is connected to a source. If the copper wire is replaced by another copper wire of the same area of cross-section but of length '4l', how will the drift velocity change? Explain your answer.
