Advertisements
Advertisements
Question
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
Solution
Young’s double slit experiment: Consider two narrow rectangular slits S1 and S2 placed perpendicular to the plane of paper. Slit S is placed on the perpendicular bisector of S1S2 and is illuminated with monochromatic light.
The slits are separated by a small distance d. A screen is placed at a distance D from S1, S2.
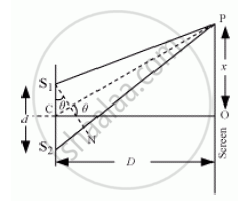
Consider a point P on the screen at distance x from O.
The path difference between the waves reaching P from S1 and S2 is:
P = S2P − S1P
Draw S1N perpendicular to S2P. Then,
P = S2P − S1P = S2P − NP = S2N
From right-angled
`DeltaS_1S^2N=(S_2N)/(S_2S_1) = sintheta`
`therefore P =S_2N=S_2S_1sintheta = d sintheta`
From ΔCOP,
When θ is small,
`sintheta≈theta≈tantheta = x/D`
`therefore P=(xd)/D`
For constructive interference,
`(xd)/D =nlambda,n=0,1,2,3,.....`
Position of nth bright fringe, `x_n = (nDlambda)/d =0,(Dlambda)/d,(2Dlambda)/d,(3Dlambda)/d,.......`
When n = 0, xn = 0, central bright fringe is formed at O.
For destructive interference,
`(xd)/D = (2n +1)lambda/2`
`or x_n = (2_n +1) (lambdaD)/(2d) = 1/2(lambdaD)/d,3/2(lambdaD)/d,5/2(lambdaD)/d,......`
Thus, alternate bright and dark fringes are formed on the screen.
RELATED QUESTIONS
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
A thin transparent sheet is placed in front of a Young's double slit. The fringe-width will _____________ .
In a Young's double slit experiment, two narrow vertical slits placed 0.800 mm apart are illuminated by the same source of yellow light of wavelength 589 nm. How far are the adjacent bright bands in the interference pattern observed on a screen 2.00 m away?
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
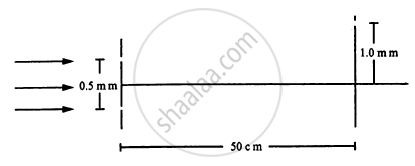
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
A beam of light consisting of two wavelengths 600 nm and 500 nm is used in Young's double slit experiment. The silt separation is 1.0 mm and the screen is kept 0.60 m away from the plane of the slits. Calculate:
- the distance of the second bright fringe from the central maximum for wavelength 500 nm, and
- the least distance from the central maximum where the bright fringes due to both wavelengths coincide.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
