Advertisements
Advertisements
Question
A thin transparent sheet is placed in front of a Young's double slit. The fringe-width will _____________ .
Options
increase
decrease
remain same
become non-uniform
Solution
remain same
On the introduction of a transparent sheet in front of one of the slits, the fringe pattern will shift slightly but the width will remain the same.
APPEARS IN
RELATED QUESTIONS
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
Write two characteristics features distinguish the diffractions pattern from the interference fringes obtained in Young’s double slit experiment.
Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A?
What is the effect on the interference fringes to a Young’s double slit experiment when
(i) the separation between the two slits is decreased?
(ii) the width of a source slit is increased?
(iii) the monochromatic source is replaced by a source of white light?
Justify your answer in each case.
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
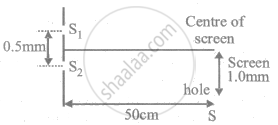
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
A beam of light consisting of two wavelengths 600 nm and 500 nm is used in Young's double slit experiment. The silt separation is 1.0 mm and the screen is kept 0.60 m away from the plane of the slits. Calculate:
- the distance of the second bright fringe from the central maximum for wavelength 500 nm, and
- the least distance from the central maximum where the bright fringes due to both wavelengths coincide.
