Advertisements
Advertisements
प्रश्न
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
उत्तर
Given: −
λ1 = 800 nm = 800 × 10−9 m
λ2 = 600 nm = 600 × 10−9 m
D = 1.4 m
d = 0.28 mm = 0.28 × 10−3 m
Let n1th maximum corresponds to λ1 coincides with n2th maximum corresponds to λ2. Then,
`n_1(lambda_1D)/d =n_2 ((lambda_2)D)/d`
`or,n_1/n^2 =lambda^2/lambda^1 = 600/800 =3/4`
The minimum integral value of n1 is 3 and of n2 is 4. Therefore, the minimum value of y is,
`y_(min) = n_1(lambda_1D)/d=(3 xx 800 xx 10^-9 xx 1.4)/((0.28) xx 10^-3)`
`y_(min) =12mm`
संबंधित प्रश्न
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
The intensity at the central maxima in Young’s double slit experimental set-up is I0. Show that the intensity at a point where the path difference is λ/3 is I0/4.
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
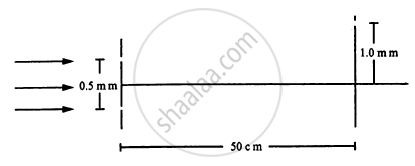
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
The force required to double the length of a steel wire of area 1 cm2, if its Young's modulus Y= 2 × 1011/m2 is:
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
