Advertisements
Advertisements
प्रश्न
In a Young's double slit experiment, two narrow vertical slits placed 0.800 mm apart are illuminated by the same source of yellow light of wavelength 589 nm. How far are the adjacent bright bands in the interference pattern observed on a screen 2.00 m away?
उत्तर
Given
Separation between two narrow slits,
\[d = 0 . 8 mm = 0 . 8 \times {10}^{- 3} m\]
Wavelength of the yellow light,
\[\lambda = 589 nm = 589 \times {10}^{- 9} m\]
Distance between screen and slit,
\[D = 2 . 0 m\]
Separation between the adjacent bright bands = width of one dark fringe
That is,
\[\beta = \frac{\lambda D}{d}...........(1)\]
\[\Rightarrow \beta = \frac{589 \times {10}^{- 9} \times 2}{0 . 8 \times {10}^{- 3}}\]
\[ = 1 . 47 \times {10}^{- 3} m\]
\[ = 1 . 47 mm\]
Hence, the adjacent bright bands in the interference pattern are 1.47 mm apart.
APPEARS IN
संबंधित प्रश्न
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
Write two characteristics features distinguish the diffractions pattern from the interference fringes obtained in Young’s double slit experiment.
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
If Young's double slit experiment is performed in water, _________________ .
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
Wavefront is ______.
In Young’s double slit experiment, what should be the phase difference between the two overlapping waves to obtain 5th dark band/fringe on the screen?
Two balls are projected at an angle θ and (90° − θ) to the horizontal with the same speed. The ratio of their maximum vertical heights is:
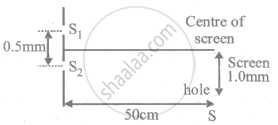
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100 cm. If a bright fringe is observed on a screen at distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
