Advertisements
Advertisements
Question
Answer the following question.
Write the conditions on path difference under which (i) constructive (ii) destructive interference occur in Young's double-slit experiment.
Solution
`I_1` = intensity of light from slit 1
`I_2` = intensity of light from slit 2
phase difference between 2 light waves = `theta = (2xΔx)/lambda`, where `Δx` = path difference resultant intensity `I` is given by,
`I = I_1 + I_2 + 2sqrt(I_1I_2) cos theta`
for constructive interference `I` should by maximum ⇒ `theta = 1`
`theta = 2npi, n = "Integer"`
`2npi = (2piΔx)/lambda`
`Δx = nlambda`
for distructive interference `I` should by minimum ⇒ `cos theta = -1`
`theta = (2n + 1)pi , n = "Integer"`
`2npi = ((2n+1)piΔx)/lambda`
`Δx = ((2n+1)lambda)/2`
APPEARS IN
RELATED QUESTIONS
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
In Young’s double slit experiment, what should be the phase difference between the two overlapping waves to obtain 5th dark band/fringe on the screen?
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
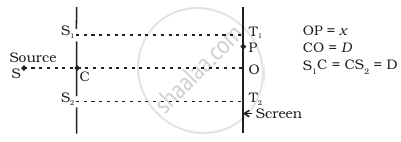
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
