Advertisements
Advertisements
Question
A Young's double slit apparatus has slits separated by 0⋅28 mm and a screen 48 cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by red light \[\left( \lambda = 700\text{ nm in vacuum} \right).\] Find the fringe-width of the pattern formed on the screen.
Solution
Given:-
Separation between two slits,
\[d = 0 . 28 mm = 0 . 28 \times {10}^{- 3} m\]
Distance between screen and slit (D) = 48 cm = 0.48 m
Wavelength of the red light,
\[\lambda_a = 700\text{ nm in vaccum} = 700 \times {10}^{- 9} m\]
Let the wavelength of red light in water = \[\lambda_\omega\]
We known that refractive index of water (μw =4/3),
\[μ_w = \frac{\text{Speed of light in vacuum}}{\text{Speed of light in the water}}\]
So, \[ \mu_w = \frac{v_a}{v_\omega} = \frac{\lambda_a}{\lambda_\omega}\]
\[ \Rightarrow \frac{4}{3} = \frac{\lambda_a}{\lambda_\omega}\]
\[ \Rightarrow \lambda_\omega = \frac{3 \lambda_a}{4} = \frac{3 \times 700}{4} = 525 nm\]
So, the fringe width of the pattern is given by
\[\beta = \frac{\lambda_\omega D}{d}\]
\[ = \frac{525 \times {10}^{- 9} \times \left( 0 . 48 \right)}{\left( 0 . 28 \right) \times {10}^{- 3}}\]
\[ = 9 \times {10}^{- 4} = 0 . 90 mm\]
Hence, fringe-width of the pattern formed on the screen is 0.90 mm.
APPEARS IN
RELATED QUESTIONS
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
In Young’s experiment interference bands were produced on a screen placed at 150 cm from two slits, 0.15 mm apart and illuminated by the light of wavelength 6500 Å. Calculate the fringe width.
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
If Young's double slit experiment is performed in water, _________________ .
The separation between the consecutive dark fringes in a Young's double slit experiment is 1.0 mm. The screen is placed at a distance of 2.5m from the slits and the separation between the slits is 1.0 mm. Calculate the wavelength of light used for the experiment.
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
Two balls are projected at an angle θ and (90° − θ) to the horizontal with the same speed. The ratio of their maximum vertical heights is:
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
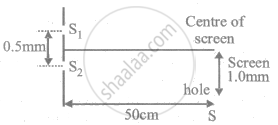
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
In Young's double slit experiment, the distance of the 4th bright fringe from the centre of the interference pattern is 1.5 mm. The distance between the slits and the screen is 1.5 m, and the wavelength of light used is 500 nm. Calculate the distance between the two slits.
